Question 867715: if one root of the polynomial p(x)=5x^2+13x+m is the reciprocal of the other find the value of m
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! It is handy to know that the product of reciprocals is always a 1. So not only are the roots of the (quadratic) polynomial reciprocals, their product is also a 1.
You may have been taught that the product of the roots of a quadratic is c/a. (If you have trouble remembering this, as I do, then see the P.S. below.)
Since we want the roots to be reciprocals and since the product of reciprocals is 1 and since the product of the roots of a quadratic is c/a, we need the following to be true:
Multiplying each side by a we get:
And since the "a" in your quadratic polynomial is 5, then the "c" must be 5, too. And since the "m" in your quadratic is where the "c" is located in quadratics in general, m = 5, too.
P.S. To figure out the formula for the product of the roots of a quadratic, you multiply the two roots from the quadratic equation:
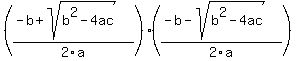
The numerators fit the  pattern so, as ugly as it may look, they are easy to multiply:
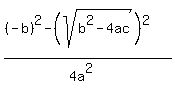
Simplifying...
|
|
|
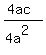
