SOLUTION: Solve by using the quadratic formula... 1. x^2-x-2=0 2. x^2=3x+12 3. 4x^2-3x+3=0 4. 5x^2-7x=1 5. 3x^2=11x+4

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Solve by using the quadratic formula... 1. x^2-x-2=0 2. x^2=3x+12 3. 4x^2-3x+3=0 4. 5x^2-7x=1 5. 3x^2=11x+4       Log On


   

Question 86271: Solve by using the quadratic formula...
1. x^2-x-2=0
2. x^2=3x+12
3. 4x^2-3x+3=0
4. 5x^2-7x=1
5. 3x^2=11x+4

Answer by scianci(186) About Me  (Show Source):
You can put this solution on YOUR website!
The quadratic formula is x+=+%28-b+%2B-+sqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29. In each case,it's just a matter of plugging in the appropriate values for a , b and c. Then simplify as much as possible. For #1, a = 1 , b = -1 and c = -2. 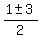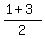So, you get :x+=+%28-%28-1%29+%2B-+sqrt%28%28-1%29%5E2-4%2A1%2A%28-2%29%29%29%2F%282%2A1%29 = %281+%2B-+sqrt%281-%28-8%29%29%29%2F2 = %281+%2B-+sqrt%289%29%29%2F2 = %281+%2B-+3%29%2F2 = %281+%2B+3%29%2F2 and %281+-+3%29%2F2 = 4%2F2 and -2%2F2 = 2 and -1
For #2, you must first set it = to 0: x%5E2 - 3x - 12 = 0. Then, a = 1 , b = -3 and c = -12. Now, proceed exactly as with #1 above. #s 4 and 5 likewise require that you first set them = 0. Then plug in your values for a , b and c and simplify. If you get an irrational square root, break it down and reduce the rational parts if possible. Otherwise just leave it as a square root. IF you get a 0 square root then the square root part dissappears and your answer is just x = -b%2F%282a%29. If you get a negative square root, then the equation has no solution. I'll let you take it from here!