Question 86270: Thanks in advance for all of your help!!
Solve by completing the square...
1.  +4x+3=0 +4x+3=0
2.  =5x+2 =5x+2
3. 2 -8x-9=0 -8x-9=0
4. 4 +2x-3=0 +2x-3=0
Answer by scianci(186)   (Show Source): (Show Source):
You can put this solution on YOUR website! When completing the square, you want to isolate the constant. For #1, then, you'd have:  + 4x = -3. + 4x = -3.
The next step, if applicable, is to factor out the lead coefficient [Not necessary in this case ; I'll demonstrate it in solving #3]
Then, divide the linear coefficient, in this case 4, by 2:  = 2 = 2
Then, square the result: 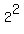 = 4 = 4
Add this to both sides of the equation:
 + 4x + 4 = -3 + 4 + 4x + 4 = -3 + 4
Now, factor the left side. It is a perfect-square trinomial which is what completing the square creates, so it'll factor as the square of a binomial:
(x + 2)^2 = 1
Take square roots of both sides:
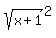 = = 
x + 1 = 
x + 1 = 
Solve each equation individually:
x + 1 = 1 , x + 1 = -1
x = 0 , x = -2
Same idea for #2 ; isolate the constant:  - 5x = 2 - 5x = 2
Then proceed exactly as in #1 above. I'll let you finish it.
For #3, start off the same way, by isolating the constant:
2 -8x = 9 -8x = 9
Next, factor out the lead coefficient:
2(x^2 - 4x) = 9
Then, complete the square on the  - 4x part: - 4x part:
 = -2 ; = -2 ; 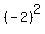 = 4 = 4
2(x^2 - 4x + 4) = 9 + 2(4) [don't forget the 2 that got factored out at the start]
2(x - 2)^2 = 17
(x - 2)^2 = 17/2
x - 2 = 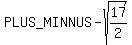
x - 2 = 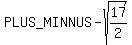 * *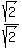
x - 2 = 
x = 2
#4 proceeds in a similar manner
|
|
|