Question 855009: ok so I got a question today in math foundations 20... I have to sketch a graph of a quadratic equation but I don't have a equation he gave me just information. I only know the axis of symmetry, x=3 the vertex is (3,5) and finally the y-intercept = (0,8) I only got that no equation how to I graph that? and what would the equation be?
Found 2 solutions by stanbon, josgarithmetic:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! the vertex is (3,5) and finally the y-intercept = (0,8) I only got that no equation how to I graph that?
-----------
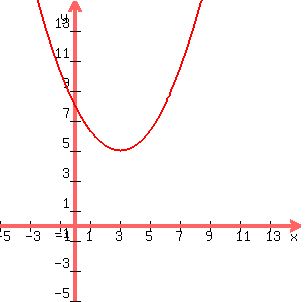
Plot those points.
Sketch a parabola opening upward from (3,5) and passing thru (0,8)
-------
By symetry along x = 3, the parabola also passes thru (6,8)
Form: y = ax^2 + bx + c
----
Equations:
Using (0,8) you get:: 0 + 0 + c = 8
Using (6,8) you get:: 36a+ 6b + c = 8
Using (3,5) you get:: 9a + 3b + c = 5
===========================================
Solve the system to get:
a = 1/3
b = -2
c = 8
=========
Equation:
y = (1/3)x^2 - 2x + 8
--------------------------------

=======================================================
Cheers,
Stan H.
=====================
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Understand the standard form for a quadratic (or at least a parabolic) equation.
 ; ;
vertex is (h,k), and this occurs on the symmetry axis (for a parabola).
The factor, a, is information about stretching or shrinking, in this form, vertically. The form shown has a vertical symmetry axis.
According to what you are given, you can use that data to fill the standard form equation. If symmetry axis is x=3, then the parabola opens either upward or downward and the vertex is on this axis.

and use the given y-intercept to help find a.
-
First, solve for a.


Substitute with (0,8).



-
EQUATION: 
The parabola is vertical, has a minimum, vertex of (3,5); the coefficient on the leading term came from knowing the y intercept.
|
|
|