Question 852341: I am really bad at these types of problems and my teacher is terrible at explaining. Can someone please help me with this one.
Suppose the revenue and cost function for a company is given by:
R(q)=-.01q^2+30q+7000
C(q)=5000+25q
Respectively.
a.)Find the profit function.
b.)How many units do we have to produce and sell to reach max[R].
c.)What is the max[R]?
d.)What is the fixed cost?
e.)What is the variable cost?
f.)Is the cost function a linear function or a quadratic function?
g.)What is/are the break-even point(s)?
I know it's a lot but I would really appreciate the help I'm honestly just not getting this. Please and thank you!
Found 2 solutions by josgarithmetic, josmiceli:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Revenue is the money that comes in.
Cost is the money that goes out.
Profit is the difference 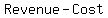 . .
(c)
Find the maximum point, or the vertex. The function value there is the maximum revenue. You could use the general solution for a quadratic equation to help find the maximum point, which will be in the middle of the horizontal axis intercepts. You could also Complete the Square to put the revenue function into standard for and read the vertex directly from the standard form. Already plenty of resources exist for understanding this, including what is completing the square? and solve quadratic by completing the square
(d)
Look at the constant term in the cost function. THAT is the fixed cost. This is the amount not dependant on q.
(e)
If you understand d, then you understand this one.
(f)
Too obvious. What's the degree of the function?
(g)
Break-even when when cost value equals revenue value; for profit of zero.
People look at symbols, read descriptions, and then try to make things more complicated than they really are. We do not know why any revenue might fit a quadratic model or why a cost might fit a linear model, or why either might fit whatever model were found; but when we have the model, we can just use it.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The revenue,  , is what you take in , is what you take in
from selling whatever you're selling
---------------------------------
The Cost, 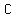 , is all of the expenses , is all of the expenses
paid out so you can sell your products
----------------------------------
The Profit,  , because if , because if
Revenue is not greater than Cost, then
you are losing money
-----------------------------------
You are given:


According to what I just stated,

----------------------------


 ( profit function ) ( profit function )
--------------------------------------------
To find  , you need to find the point ( q, R ) where , you need to find the point ( q, R ) where
the function  reaches a peak reaches a peak
The formula to use is:
 where: where:






1500 units need to be produced to reach 
-----------------------------------------------
To find 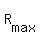 back into back into 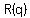





The Revenue peaks at $29,500
-----------------------------
The cost, 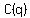 , is split into: , is split into:
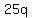 is variable is variable
 is fixed is fixed
--------------------------
The Cost function is linear because the
highest power that  is raised to in is raised to in
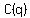 is one is one
------------------------------------
The break-even point is where  , or , or
where the revenue just barely equals the Cost
so, to find this point, I can say:
 , or, whatis the same thing: , or, whatis the same thing:


You can use the quadratic formula:










This is the number of items sold at the break-even point
Here are the plots of:
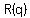
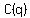
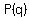

The bottom parabola is the Profit function, and you can
see that it is zero ( break-even point ) just below where
Revenue = Cost.  as you can see as you can see
( unless I miscalculated )
Hope this helps
|
|
|