SOLUTION: 5x^3+30x^2-15x

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: 5x^3+30x^2-15x      Log On


   

Question 852178: 5x^3+30x^2-15x
Found 2 solutions by Fombitz, josh_jordan:
Answer by Fombitz(32388) About Me  (Show Source):
Answer by josh_jordan(263) About Me  (Show Source):
You can put this solution on YOUR website!
In order to solve for x, the first thing you want to do is set this expression equal to 0:

5x%5E3%2B30x%5E2-15x=0

Next, since each of these terms have 5x in common, we can factor 5x out of the equation, giving us:

5x%28x%5E2%2B6x-3%29=0

Setting each of these terms equal to 0, gives us:

5x=0 and x%5E2%2B6x-3=0

With 5x = 0, we can quickly see that x = 0, so, we know that one of the values of x is 0.

Now, in order to find the other two values of x, we need to use the quadratic formula on our second term, x^2 + 6x - 3 = 0:

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ ----->

x+=+%28-6+%2B-+sqrt%28+6%5E2-4%2A1%2A-3+%29%29%2F%282%2A1%29+ ----->

x+=+%28-6+%2B-+sqrt%28+36%2B12+%29%29%2F%282%29+ ----->

x+=+%28-6+%2B-+sqrt%28+48+%29%29%2F%282%29+ ----->

x+=+%28-6+%2B-+4%2Asqrt%28+3+%29%29%2F%282%29+

Now, we can factor a 2 out of the numerator, since 2 is a factor of both -6 and +- 4:

x+=+%282%28-3+%2B-+2%2Asqrt%28+3+%29%29%29%2F%282%29+ ----->

x+=+-3+%2B-+2%2Asqrt%28+3+%29+

We now have our 3 values of x: 0,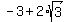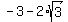-3%2B2%2Asqrt%283%29,-3-2%2Asqrt%283%29