SOLUTION: A sequence of diagrams is formed by drawing equilateral triangles, each side is 1 cm. They give me 3 diagrams. 1. Triangle 2. Big triangle with smaller on inside ( makes 4 tria

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A sequence of diagrams is formed by drawing equilateral triangles, each side is 1 cm. They give me 3 diagrams. 1. Triangle 2. Big triangle with smaller on inside ( makes 4 tria      Log On


   

Question 838176: A sequence of diagrams is formed by drawing equilateral triangles, each side is 1 cm.
They give me 3 diagrams.
1. Triangle
2. Big triangle with smaller on inside ( makes 4 triangles - 9 lines)
3. Big with smaller triangles ( 18lines)
Question:
The formula for the TOTAL number of one cm lines needed to draw ALL OF THE FIRST n DIAGRAMS is an^3+bn^2+n
Find the values of a and b
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
--> -->
All you have to do to draw each row of triangles is draw the numbered triangles.
The ones without numbers get formed by the sides of the numbered triangles.
You draw 1 triangle for row/diagram number 1.
You add 2 triangles for row 2 in diagram number 2, for a total of 3 triangles.
You add 3 triangles for row 3 in diagram number 3, for a total of 6 triangles.
Each triangle drawn takes 3 line segments.
The first diagram used 3%2A1=3%29%29%29+segments.%0D%0AThe+second+diagram+used+%7B%7B%7B3%2A3=9 segments, and the third used 3%2A6=18 .
The pattern above continues.
We could calculate formulas for the total number of triangles in the nth diagram, the number of segments in the nth diagram, and the total number of segments in the first diagram, but we do not need to.
The problem GIVES us the formula (sort of).
If it is true,
in the first 1 diagram, there are
a%2A1%5E3%2Bb%2A1%5E2%2B1=a%2Bb%2B1 segments.
We know that number is 3 , so
a%2Bb%2B1=3 --> a%2Bb=3-1 --> a%2Bb=2 .
In the first 2 diagrams, there should be a total of
a%2A2%5E3%2Bb%2A2%5E2%2B2=8a%2B4b%2B2 segments.
We know that there are 3%2B9=12 segments, so
8a%2B4b%2B2=12 --> 8a%2B4b=12-2 --> 8a%2B4b=10 --> 4a%2B2b=5
Now we have a system of two linear equations in a and b that is really easy to solve:
system%28a%2Bb=2%2C4a%2B2b=5%29 --> highlight%28system%28a=1%2F2%2Cb=3%2F2%29%29 .
So the total number of segments in the first n diagrams is
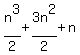
n%5E3%2F2%2B3n%5E2%2F2%2Bn
Just for curiosity, let's se if it works for n=3 .
It would be
3%5E3%2F2%2B3%2A3%5E2%2F2%2B3=27%2F2%2B27%2F2%2B3=27%2B3=30
Since we had 3 , 9 , and 18 segments in the first 3 diagrams, and 3%2B9%2B18=30, the formula works for n=3 .

Could we have deduced that formula?
Yes, laboriously, but what was required was much simpler and easier.
To arrive at that formula, we could start by calculating the number of segments in the nth diagram
You add n triangles for row n in diagram number n .
The total number of triangles drawn to make diagram number n%7D%7D+is%0D%0A%7B%7B%7B1%2B2%2B3%2B%22.....%22%2Bn=n%28n%2B1%29%2F2 , and that means
3n%28n%2B1%29%2F2=%283%2F2%29n%5E2%2B%283%2F2%29n 1-cm line segments (sides of those triangles).
sum%28%283%2F2%29k%5E2%2B%283%2F2%29k%2C+k=1%2C+k=n+%29 is a sum of polynomials with degree 2,
so it must be a polynomial of degree 3.
We write SUM%5Bn%5D=sum%28%283%2F2%29k%5E2%2B%283%2F2%29k%2C+k=1%2C+k=n+%29=an%5E3%2Bbn%5E2%2Bcn%2Bd .
From SUM%5Bn%5D-SUM%5Bn-1%5D=%283%2F2%29n%5E2%2B%283%2F2%29n we would find out a , b , c , and d .