SOLUTION: Hi, So I missed my Pre-Ap Algebra II class, and I was wondering how I would be able to find a quadratic function that includes each set of Values. So, the question that I was w

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Hi, So I missed my Pre-Ap Algebra II class, and I was wondering how I would be able to find a quadratic function that includes each set of Values. So, the question that I was w      Log On


   

Question 828362: Hi,
So I missed my Pre-Ap Algebra II class, and I was wondering how I would be able to find a quadratic function that includes each set of Values.
So, the question that I was working on gave me three points, which are (1,-2),(2,-2), and (3,-4).
I did look in the textbook, and I attempted to try each. This is what I have so far.
*y=ax^2+bx=c
-2=A(-1)^2+b(1)+c
-2=a+b+c
*y=ax^2+bx=c
-2=a(2)^2+b(2)+c
-2=4a+2b+c
*y=ax^2+bx=c
-4=a(3)^2=b(3)=c
-4=9a+3b+c
So thats what I have so far, but in the example i noticed it said "use one of the methods in chap.3" and solve. Im not sure what to do after all of that from above. I just want to know which way is the easiest and will help me with my following homework problems. I was also wondering if there was any way to check it to make sure my answer will be right with this and the upcoming problems that I have to solve.
Thank you so much for your time and help
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Some of your steps are not clear. You could use the given three points to form three equations with unknown coefficients and use very simple linear algebra skills to find the values of these coefficients.

You can also use the quality of symmetry for a quadratic equation of a parabola, and find the x value of the center, so you know the vertex is on that line of symmetry. Having points (1,-2) and (2,-2), you know that because of symmetry, this parabola has a vertex on x=3%2F2.

Looking at the other given point on the parabola, (3,-4), you understand that the "a" coefficient on x^2 is negative; the value of the function decreases as x moves away from x=3%2F2, and the function has a MAXIMUM at x=3%2F2.

LOOK AT the standard form equation for your so-far-unfinished function.
y=a%28x-3%2F2%29%5E2%2Bk.
Plug in the point (3,-4).
-4=a%283-3%2F2%29%5E2%2Bk, and simplify.
-4=a%289%2F4%29%2Bk
-16=9a%2B4k
9a%2B4k=-16-----nice linear equation.
NOW, use that same standard form equation and substitute for either (1,-2) OR (2,-2). No matter which; just choose either.
-2=a%282-3%2F2%29%5E2%2Bk
-2=a%281%2F4%29%2Bk
-8=a%2B4k
a%2B4k=-8----another very nice linear equation.
-
Solve this system of two linear equations in the unknowns, a and k.
------------------------
9a+4k=-16
---------------------
a+4k=-8
------------------------

Once solved for a and k, finish your standard form equation of y=a%28x-3%2F2%29%5E2%2Bk



-----------------------------
note: a=-1 and therefore k=-7%2F4, easily found through Elimination Method. Finished standard form parabola, highlight%28y=-%28x-3%2F2%29%5E2-7%2F4%29.

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Hi,
So I missed my Pre-Ap Algebra II class, and I was wondering how I would be able to find a quadratic function that includes each set of Values.
So, the question that I was working on gave me three points, which are (1,-2),(2,-2), and (3,-4).
I did look in the textbook, and I attempted to try each. This is what I have so far.
*y=ax^2+bx=c
-2=A(-1)^2+b(1)+c
-2=a+b+c
*y=ax^2+bx=c
-2=a(2)^2+b(2)+c
-2=4a+2b+c
*y=ax^2+bx=c
-4=a(3)^2=b(3)=c
-4=9a+3b+c
So thats what I have so far, but in the example i noticed it said "use one of the methods in chap.3" and solve. Im not sure what to do after all of that from above. I just want to know which way is the easiest and will help me with my following homework problems. I was also wondering if there was any way to check it to make sure my answer will be right with this and the upcoming problems that I have to solve.
Thank you so much for your time and help


Your 3 equations in 3 unknowns are correct, up to this point. 

 

You can use ELIMINATION (see below) to solve for the variables, and determine the quadratic equation.

You can also use MATRICES to solve for the variables, if you're familiar with this method.



 a +  b + c = - 2 -------- eq (i)

4a + 2b + c = - 2 -------- eq (ii)

9a + 3b + c = - 4 -------- eq (iii) 



- 3a – b = 0 ------- Subtracting eq (ii) from eq (i) ------ eq (iv) 

- 5a - b = 2 ------- Subtracting eq (iii) from eq (ii) ------ eq (v)

      2a = - 2 ----- Subtracting eq (v) from eq (iv)

       a = 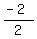%28-+2%29%2F2, or highlight%28a+=+-+1%29 

- 3(- 1) – b = 0 ------- Substituting 1 for a in eq (iv) 

       3 – b = 0 

         - b = - 3

           b = %28-+3%29%2F-+1, or highlight%28b+=+3%29

 1 + (3) + c = - 2 ------- Substituting 1 for a, and – 3 for b in eq (i)

   1 + 3 + c = - 2 

       4 + c = - 2

           c = - 2 - 2, or highlight%28c+=+-+4%29

With a being - 1, b being 3, and c being - 4, the equation: y+=+ax%5E2+%2B+bx+%2B+c+ becomes:

y+=+-+1%28x%5E2%29+%2B+3%28x%29+%2B+-+4

Quadratic equation thus formed: highlight_green%28y+=+-+x%5E2+%2B+3x+-+4%29



To check if this is the correct equation, just substitute each coordinate point into the equation, and each 

equation should prove true.



You can do the check!! 



Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.

Further help is available, online or in-person, for a fee, obviously. 

	

For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams, 

GENERAL MATH QUESTIONS, MATH HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,

Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE, GRE, CLEP,

and the GED, you can visit: http://asvabstudyzone.freeforums.net/.