

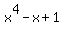
The graph of that is gotten by plotting
(-2,19), (-1,3), (0,1), (1,1), (2,15)
 The slope of a tangent line at a point IS the derivative
at that point. So we find
The slope of a tangent line at a point IS the derivative
at that point. So we find 


 Evaluate that at x=1
Evaluate that at x=1


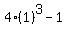

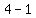

 Now we find the equation of the line with slope m=3 that
goes through to point where x=1. We must find the y-coordinate,
by substituting x=1 in the original equation for the graph:
Now we find the equation of the line with slope m=3 that
goes through to point where x=1. We must find the y-coordinate,
by substituting x=1 in the original equation for the graph:


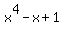


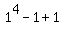


 Use the point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = (1,1)
y-1 = 3(x-1)
y-1 = 3x-3
y = 3x-2 <---answer
Find the points on that tangent line (0,-2), (1,1), (2,4), (3,7)
and graph it as a check to make sure it looks like it's tangent
to the curve:
Use the point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = (1,1)
y-1 = 3(x-1)
y-1 = 3x-3
y = 3x-2 <---answer
Find the points on that tangent line (0,-2), (1,1), (2,4), (3,7)
and graph it as a check to make sure it looks like it's tangent
to the curve:
 Edwin
Edwin