SOLUTION: A parabola is defined as a set of points that are equidistant from a given line (called the directrix of the parabola) and a given point (called the focus) of the parabola. Find

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A parabola is defined as a set of points that are equidistant from a given line (called the directrix of the parabola) and a given point (called the focus) of the parabola. Find      Log On


   

Question 826426: A parabola is defined as a set of points that are equidistant from a given line (called the directrix of the parabola) and a given point (called the focus) of the parabola.
Find an equation that describes all the points that are the same distance from the x-axis and the point (0,2).
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
The points on the x axis would be like (x,0), because y is zero on the x-axis. The vertex point is directly in the middle of (0,2) and (x,0), being at (0,1).

You are looking for distances from (x,y) to (0,2) to be equal to distances from (x,y) to (x,0). Use the Distance Formula for expressions of these two distances and equate them.

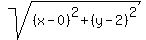
sqrt%28%28x-0%29%5E2%2B%28y-2%29%5E2%29
sqrt%28x%5E2%2By%5E2-4y%2B4%29
'
The other distance,
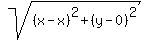
sqrt%28%28x-x%29%5E2%2B%28y-0%29%5E2%29
sqrt%280%2By%5E2%29
sqrt%28y%5E2%29
'
sqrt%28x%5E2%2By%5E2-4y%2B4%29=sqrt%28y%5E2%29
Square both sides,
x%5E2%2By%5E2-4y%2B4=y%5E2
x%5E2-4y%2B4=0
x%5E2%2B4=4y
4y=x%5E2%2B4
highlight%28y=%281%2F4%29x%5E2%2B1%29

Graph might help:
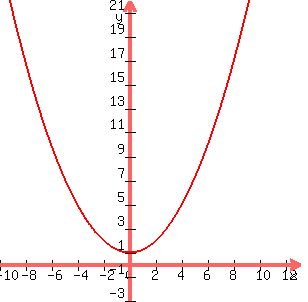
graph%28300%2C300%2C-10%2C13%2C-3%2C22%2C%281%2F4%29x%5E2%2B1%29

Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!


Every one of those vertical green lines from the curve down to the
x-axis must be equal to the slanted line that it's connected to that
goes to the point (0,2). Not only those but also an infinite number of 
possible pairs of green lines that COULD be drawn.

Let's pick one of those pairs of green line at random, and label it
with the variable coordinates (x,y).  the bottom of the green line
must have the same x-coordinate, so it has the coodinates (x,0).





We use the distance formula

d = √(x2-x1)²+(y2-y1)²

to set the distance from (x,y) to (x,0) equal to the distance between
(x,y) to (0,2)

 
    √(x-x)²+(0-y)² = √(0-x)²+(2-y)² 

Squaring both sides takes away the radicals

     (x-x)²+(0-y)² = (0-x)²+(2-y)²

        (0)²+(-y)² = (-x)²+(2-y)²

              0+y² = x²+(4-4y+y²)

                y² = x²+4-4y+y²

                 0 = x²+4-4y

                4y = x²+4

                 y = 1%2F4x²+1

That's the equation.

Edwin