Question 824460: what must be added to 7x^2-10x to make a perfect square. Thanks
Found 2 solutions by richwmiller, jsmallt9:
Answer by richwmiller(17219)   (Show Source):
You can put this solution on YOUR website! 25/49
to find it first divide by 7
and we get
x^2-10/7x
take half of 10/7 which is 5/7 and square it 25/49
x^2-10/7x+25/49=25/49
(x-5/7)^2=25/49
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website! The way you worded the problem leads me to think that it is different from the usual problems of this type. So I'm going to do this two ways: one to match the way you worded the problem and another to match the types of problems that are often given.
To create a perfect square one must first be familiar with the perfect square patterns:Since your expression has a minus in front of 10x, we will be using the second pattern. What we will do is start matching what we have compared to the pattern and then figure out what is missing in order to complete the expression so that it matches the full pattern.
The pattern starts with  and our expression starts with  . So if we are to match the pattern:
Solving for a we get:
Now we want our second term, 10x, to match the pattern's second term. So
Substituting the expression we got for a above:
Now we solve for b. Dividing both sides by  :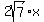
The x's cancel as does a factor of 2. This leaves us with:
Now we need to figure out what third term is needed to make the expression match the full pattern. The pattern says that the third term should be  . Using the expression we got for b:
which simplifies to:
So this is the third term we need to make it a perfect square. Using the "a" and "b" from above:
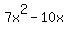
Add a strange-looking zero:
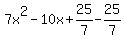
Group the part that matches the pattern:
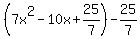
Rewrite the grouped expression as a perfect square:
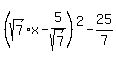
Then the specific answer to "what must be added to 7x^2-10x to make a perfect square" is: 25/7.
The way these problems are usually described as something like "Rewrite this expression in terms of a perfect square." For this we start by factoring out the "a" (if it, like the 7 we have, is not a perfect square):
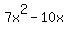
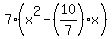
Now we complete the square inside the parentheses. This time our "a" is simply "x". Matching the second term to the pattern:
Substitute for "a":
Dividing by 2x:
Then  Now comes the tricky part. We want the 25/49 to be the third term ... inside the parentheses of
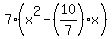
So it looks like we would be adding 25/49 to the expression. But that would be wrong! There is a 7 in front of the parentheses. So anything added inside the parentheses is actually being added 7 times! So to balance the addition of 7 25/49's we must subtract the same amount:
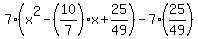
Rewriting the perfect square and simplifying the multiplication at the end:
This approach is easier because there are no square roots. But it is harder, too, because we had to realize that 7 25/49's were being added when we added 25/49 inside the parentheses.
P.S. Often these problems are not just expressions, they are equations. For example:
When this is true, we can still add a "weird zero" like we did above or we can add the needed third term to both sides of the equation instead:
etc.
P.P.S. In the first solution, the "b" was  . With a square root in the denominator, this is often not an acceptable form. It should be rationalized:
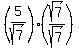
which simplifies to:
|
|
|
