Question 81771: Problem
Find three consecutive integers such that the sum of their squares is 77.
This is what I have, but not sure.
x^2 + x^2 + x^2 = 77 I don't know where to go from here. Thank you for your help.
Found 2 solutions by jim_thompson5910, bucky:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x=1st #, y=2nd #, z=3rd #
Since you have consecutive integers, this means the integers are right next to each other. For instance, 1,2, and 3 are all consecutive integers. If x=1, then y=2, and z=3. So if you wanted them all in terms of x, you would say:
x=1, y=x+1, z=x+2
Since if you plug in x=1 into x+2, you get z=3. So the same applies to this problem.
So now we're adding the squares of these numbers to get 77 like this:

But we can write y as  and z as and z as 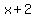 so we can replace y and z: so we can replace y and z:

 Foil the two parenthesis separately Foil the two parenthesis separately
 Combine like terms Combine like terms
 Subtract 77 from both sides Subtract 77 from both sides

Now that we have a quadratic, lets use the quadratic formula to solve for x:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=900 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 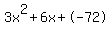 can be factored: can be factored:

Again, the answer is: 4, -6.
Here's your graph:
 |
So we have 2 possible numbers for our first number.
Now lets check our first possible answer x=4:
Lets find our 2nd number using x=4:

 Plug in x=4 Plug in x=4

So our 2nd number is 5
Lets find our 3rd number using x=4

 Plug in x=4 Plug in x=4

So our 3rd number is 6
So our 3 numbers are 4,5,6
Check:
 Plug in x=4,y=5,z=6 Plug in x=4,y=5,z=6

 works works
Now lets check our other possible answer x=-6:
Lets find the 2nd number using x=-6

 Plug in x=-6 Plug in x=-6

So our 2nd number is -5
Lets find our 3rd number using x=-6

 Plug in x=-6 Plug in x=-6

So our 3rd number is -4
So our 3 numbers are -6,-5,-4
Check:
 Plug in x=-6,y=-5,z=-4 Plug in x=-6,y=-5,z=-4

 works works
So we have 2 sets of numbers that work. We have one set
4,5,6
and we also have
-6,-5,-4
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first thing to do is to let x be the first integer. Then the next consecutive integer
is 1 number higher or x + 1. And the next consecutive integer after that is (x+1) + 1 or
x + 2.
.
The squares of these numbers are:
.
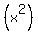
.

.

.
If you add these three squares together you get:
.
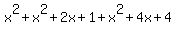
.
Combine the like terms and you get:
.

.
This reduces to:
.
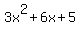
.
This is the sum of the squares and the problem tells you that this sum equals 77. So
the equation becomes:
.

.
Put this into standard quadratic form by subtracting 77 from both sides to get:
.

.
Since this is in standard quadratic form, you can solve it by using the quadratic
formula. Although it may be difficult to recognize, the left side of this equation can
be factored:
.

.
Divide both sides by 3 to reduce the equation to:
.

.
This equation will be true if one of the factors is zero because a multiplier of zero on the
left side will make the left side equal to zero, just as the right side is.
.
So solve this equation by setting each factor equal to zero.
.

.
Solve by adding 4 to both sides to get  . This would mean that the next two . This would mean that the next two
consecutive integers are 5 and 6.
.
Now set the second factor equal to zero:
.

.
Solve by subtracting 6 from both sides to get  . This makes the next two . This makes the next two
consecutive integers (x+1 and x + 2) equal to -5 and -4.
.
So we have two possibilities. One solution is 4, 5, and 6. The other solution is -6, -5,
and -4.
.
Let's check them out.
.

.
That works. Now:
.

.
Although it's a little more difficult to think about, -6, -5, and -4 are three consecutive
integers that also work.
.
Hope this helps you to understand the problem.
|
|
|