Question 795063: Find the vertex of each equation ! PLEASE HELP SOMEONE !!!
1. h(x) = (x + 2)2 – 1
2. h(x) = (x + 1)2 – 2
3. h(x) = (x - 2)2 - 1
4. h(x) = (x - 1)2 – 2
5. h(x) = (x + 2)2 + 1
6. h(x) = (x + 1)2 + 2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The vertex is right there, in front of your eyes.
I'll show you how to look for it.
1.  is is  when when  , ,
because then  . .
For all other values of  , ,
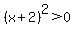 and and  . .
So (-2,-1), with  and and  is the minimum and the vertex. is the minimum and the vertex.
2.  has a minimum and vertex at (-1,-2), because has a minimum and vertex at (-1,-2), because
when   takes the minimum value takes the minimum value

3.  has a maximum and vertex at (2,-1). has a maximum and vertex at (2,-1).
4.  has a maximum and vertex at (1,-2) has a maximum and vertex at (1,-2)
5.  has a maximum and vertex at (-2,1) has a maximum and vertex at (-2,1)
6.  has a maximum and vertex at (-1,2) has a maximum and vertex at (-1,2)
NOTES:
If you had a minus sign in front of that square, as in
 the vertex, at (3,4) in this case, would be a maximum, because for the vertex, at (3,4) in this case, would be a maximum, because for  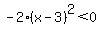 and and 
When they give you the function as
 you will have to transform it to the form given above you will have to transform it to the form given above
 to find the vertex. to find the vertex.
You an write your exponents with a "^" in front, as in
h(x) = (x + 1)^2 + 2 , and everyone will know you mean 
|
|
|