Question 785476: Please help me to solve this quadratic equation 
Answer by Trontor(4)   (Show Source):
You can put this solution on YOUR website!
Firstly, expand the 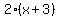 using the distributive law, this makes our equation 
Since you didn't provide a method, I will do it the easiest way, the quadratic formula.
From here you can say that x = -6 straight away, but using the QUADRATIC FORMULA:
The standard formula that applies to the quadratic formula is 
a = Coefficient of  b = Coefficient of  c = the single number value
a = 0 ( ) b = 1 ( ) c = 6
Quadratic Formula = 
WE CANNOT DO THIS! AS 2*a = 0 , which means we CANNOT divide by zero.
I will assume that your equation is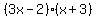 
Which is expanded to  which is fine for a quadratic equation.
a = 3 b = 7 c = -6
Now we substitute the a, b, and c values that are in your equation into this quadratic formula so it can return 2, (maybe 1 in this case) values of x.
THEREFORE
I personally think you mistyped the equation, it was 
not .
Thanks, remember to mark this as your solution if I got it!
|
|
|
