SOLUTION: Write the function in vertex form. y=x^2-3x+6

We want to get y = a(x-h)²+k 

y = x²-3x+6 in the form 

Put brackets around the first two terms on the
right,

y = [x²-3x]+6

 and since the coefficient of x² is 1 put 1
in front of the parentheses. Normally you
would factor out the coefficient of x²:

y = 1[x²-3x]+6

We complete the square inside the brackets:

1. Multiply the coefficient of x, which is -3
   by , getting .
2. Square  getting  =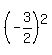 
3. Add 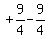, which is really 0, inside the
   brackets:

y = 1[x²-3x+-]+6

Factor the first three terms inside the bracket like this
             x²-3x+ = (x-)(x-) = (x-)²

y = 1[(x-)²-]+6

Remove the bracket

y = 1(x-)²-+6 

Write the 6 as 

y = 1(x-)²-+

y = 1(x-)²+ 

y = a(x-h)²+k

The vertex is (h,k) = (,)

Edwin