Question 76446This question is from textbook Beginning Algebra
: I need help on page #575 on question #20. I need to solve the roots of each quadratic equation using the factoring method, and place the equation in standard form before factoring:
X^2=10x-24
Thanks for your time. =)
This question is from textbook Beginning Algebra
Found 2 solutions by checkley75, bucky:
Answer by checkley75(3666)   (Show Source):
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! Given:
.
Task: Arrange in standard form and solve for x by factoring
.
The standard form of a quadratic equation is:
.
.
The key features of this form are:
(1) all the terms are on the left side and zero is on the right side and
(2) the terms on the left side are arranged in descending powers of x. So the first term
contains  , the second term contains  , and the third term is just a constant.
.
To get the given equation in standard form we need to eliminate the two terms on the right
side by subtracting 10x - 24. But if you subtract 10x - 24 from the right side, you must
also subtract 10x - 24 from the left side to keep the equation in balance. When you subtract
10x - 24 from both sides the equation becomes:
.
.
The rule to remove a set of parentheses preceded by a minus sign you remove the minus sign
and the parentheses but you need to change the sign of each term in the parentheses.
Applying this rule to the parentheses on the left side you get:
.
.
Since we already have the terms arranged in descending powers of x we have things in
the standard form. Therefore we have met the first requirement of the problem. Now we have
to solve for values of x that will make the left side of the equation equal zero.
.
Since the multiplier of the term is 1, the factors will take the form:
.
(x __ ___)*(x __ ___)
.
where the underlines in each set of parentheses represent a missing sign and a missing number.
.
The missing numbers in the two sets of parentheses must be factors of 24, because when
they are multiplied together they must equal +24. Because the product must be positive
the two numbers must both be positive or both be negative. If one was positive and one
was negative, their product would be -24, and we need it to be +24. Now we look at the
middle term on the left side. Its multiplier is -10. We know that the two factors
of 24 that we use must have a product of +24 and a sum of -10. From this we can tell that
the factors must both be negative (so their product is +24 and their sum is -10). Now
we know that the missing factors of 24 must add to be -10. The factors of 24 are:
(24 and 1), (12 and 2), (8 and 3), and (6 and 4). The only set of factors that adds up
to 10 is 6 and 4. And both must be negative so they add to be -10 and multiply to be +24.
.
So we now know that the factors of the left side are:
.
.
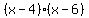
and the equation, therefore, is:
.
.
Note that this equation will be true if either of the factors is equal to zero, because
multiplying the left side by 0 will make it equal to the right side.
.
So we know that either  or  will make the equation true. So solve
these two equations and you get  and  as the two values of x that
will make equal the left and right sides of the original equation you were given.
.
Try it for x = 4. The original equation becomes:
.
.
This expands to become:
.
.
which simplifies to
.
.
This verifies that x = 4 is a correct solution. You can do the same sort of checking
for x = 6.
.
Hope this helps you to understand the problem a little better and helps you to understand
the method you can use to factor a quadratic if the multiplier of the term is 1.
|
|
|
