Question 750248: A parabola shaped tunnel is 10m high at the centre and spans 18m wide at the base. A 7.5 m high vehicle needs to use the tunnel;, what is the maximum width of the vehicle that can fit through the tunnel?
I need to draw a diagram to represent the tunnel on a coordinate number plane , and find the equation of the parabola. using algebra and coordinate geometry to determinate the maximum width of the truck
I try to solve this problem many times but my results seems to be wrong, please help me I'm so stuck
Ally
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! Think of this as a parabola that opens downward, and
the base, or the road, is the x-axis. The y-axis goes
through the maximum height. The x-intercepts are at
( 9,0 ) and ( -9,0 ), making the base 18 wide
-------------------
The vertex of the parabola is at ( 0,10 )
Find the equation of the parabola
It will have the general form
The x-coordinate of the vertex is at
 I have stated that 
So far, I have
-----------------
Also, the vertex is at ( 0,10 ), so I can say
 , and so far I have
------------------
The other points I have are ( -9,0 ) and ( 9,0 )
If I say 
If  or  , then
---------------
The whole equation is:
------------------------
Here's the plot:
-------------------------
What they want to know is:
What is  when  , and
What is  when
Then you find 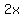 , which is the width of the truck.
-----------------------
The maximum width of the truck is 9 m
---------------
check:
OK
|
|
|
