find the quadratic function which takes the value 41 at x=-2
y = Ax²+Bx+C
41 = A(-2)²+B(-2)+C
41 = A(4)-2B+C
41 = 4A-2B+C
first equation: 4A-2B+C = 41
and the value 20 at x=5
y = Ax²+Bx+C
20 = A(5)²+B(5)+C
20 = A(25)+5B+C
20 = 25A+5B+C
second equation: 25A-5B+C = 20
and is minimized at x=21
A parabola has its lowest point, that is, it is
minimized at its vertex. Its vertex has as its
x-coordinate the value 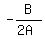 so we set
that = 21
so we set
that = 21
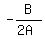 = 21
Cross-multiplying:
-B = 42A
-42A - B = 0
42A + B = 0
third equation: 42A + B = 0
eq. 1 4A-2B+C = 41
eq. 2 25A+5B+C = 20
eq. 3 42A+ B = 0
Multiply eq. 1 by -1 and add it to eq. 2 to eliminate
the C's
25A+5B+C = 20
-4A+2B-C = -41
-----------------
21A+7B = -21
That can be easily divided through by 7
eq. 4 3A+ B = -3
Now we have a system with only 2 equations and
2 unknowns.
eq. 4 3A+ B = -3
eq. 3 42A+ B = 0
Multiply eq. 4 through by -1 and add to eq. 3 to ekiminate
the B's.
-3A- B = 3
42A+ B = 0
----------
39A = 3
A =
= 21
Cross-multiplying:
-B = 42A
-42A - B = 0
42A + B = 0
third equation: 42A + B = 0
eq. 1 4A-2B+C = 41
eq. 2 25A+5B+C = 20
eq. 3 42A+ B = 0
Multiply eq. 1 by -1 and add it to eq. 2 to eliminate
the C's
25A+5B+C = 20
-4A+2B-C = -41
-----------------
21A+7B = -21
That can be easily divided through by 7
eq. 4 3A+ B = -3
Now we have a system with only 2 equations and
2 unknowns.
eq. 4 3A+ B = -3
eq. 3 42A+ B = 0
Multiply eq. 4 through by -1 and add to eq. 3 to ekiminate
the B's.
-3A- B = 3
42A+ B = 0
----------
39A = 3
A = 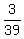 A =
A =  Since that's a nasty fraction, it will be easier to start over
and eliminate A from eqs. 4 and 3
3 goes into 42 14 times so we just have to multiply eq. 4 by
-14 and add it to eq. 3:
-42A-14B = 42
42A+ B = 0
--------------
-13B = 42
B =
Since that's a nasty fraction, it will be easier to start over
and eliminate A from eqs. 4 and 3
3 goes into 42 14 times so we just have to multiply eq. 4 by
-14 and add it to eq. 3:
-42A-14B = 42
42A+ B = 0
--------------
-13B = 42
B = 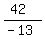 B =
B = 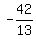 Substitute that and A =
Substitute that and A =  into eq. 1:
eq. 1 4A-2B+C = 41
4
into eq. 1:
eq. 1 4A-2B+C = 41
4 -2
-2 +C = 41
Clear of fractions by multiplying through by 13
4 + 84 + 13C = 533
88 + 13C = 533
13C = 445
C =
+C = 41
Clear of fractions by multiplying through by 13
4 + 84 + 13C = 533
88 + 13C = 533
13C = 445
C =  Those are terrible fractions, but they are correct. I
suspect you may have made a slight typo, such as typing
a sign or a digit wrong in one of your figures.
But the correct function based on the numbers you gave, is:
y =
Those are terrible fractions, but they are correct. I
suspect you may have made a slight typo, such as typing
a sign or a digit wrong in one of your figures.
But the correct function based on the numbers you gave, is:
y =  x² -
x² - 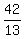 x +
x +  or if you like you can use functional notation f(x) for y:
f(x) =
or if you like you can use functional notation f(x) for y:
f(x) =  x² -
x² - 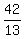 x +
x +  Edwin
Edwin