Question 746300: is there any quadratic equation which has more than two roots because i have studied so far that whatever be the highest power of the variable we have that much roots only.But someone told me that there are more than two roots in an quadratic equation.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! As far as I know, a quadratic equation has "two complex roots" that can be the same, so we would call that one double real root. There could also be two different real roots, or two different imaginary roots (no real roots).
Using the "complete the square" strategy you can get from the quadratic equation with coefficients a, b,and c
to the quadratic formula that allows you to calculate the roots:
The plus/minus sign is what gives you the two roots.
If  both roots are the same  .
If 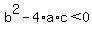 both roots cannot be calculated as real numbers, but clever mathematicians invented complex numbers (all the real numbers you know plus a lot of imaginary ones), and they are useful in technical applications.
If 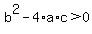 you get two different real numbers.
The quadratic function  graphs as a parabola, like these:
 As you can see, can happen fore just one value of x, for two different values of x, or for no value of x at all. That is one, two, or no real solutions.
|
|
|
