SOLUTION: Show that the quadratic function {{{y=ax^2+bx+c}}} can be written in the form {{{y-k=a(x-h)^2}}} where the point (h,k) is the vertex of the parabola an{{{ h= -b/2a}}} and {{{k= c

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Show that the quadratic function {{{y=ax^2+bx+c}}} can be written in the form {{{y-k=a(x-h)^2}}} where the point (h,k) is the vertex of the parabola an{{{ h= -b/2a}}} and {{{k= c      Log On


   

Question 744560: Show that the quadratic function y=ax%5E2%2Bbx%2Bc can be written in the form y-k=a%28x-h%29%5E2 where the point (h,k) is the vertex of the parabola an+h=+-b%2F2a and k=+c-b%5E2%2F4a
Substitute the algebratic expressions for h and k into the general equation and transpose for y
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
y-k=a%28x-h%29%5E2 Substitute the values for h and k>


y-%28c-b%5E2%2F4a%29=a%28x-%28-b%2F2a%29%29%5E2


y-c%2Bb%5E2%2F4a=a%28x%2Bb%2F2a%29%5E2


FOIL %28x%2Bb%2F2a%29%5E2


y-c%2Bb%5E2%2F4a=a%28x%5E2+%2B2bx%2F2a+%2B+b%5E2%2F4a%5E2%29


Distribute a


y-c%2Bb%5E2%2F4a=ax%5E2+%2B2abx%2F2a+%2B+ab%5E2%2F4a%5E2%29


Cancel where possible


y-c%2Bb%5E2%2F4a=ax%5E2+%2Bbx+%2B+b%5E2%2F4a%29


Add c to both sides. Subtract 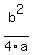b%5E2%2F4a from both sides.


y=ax%5E2%2Bbx%2Bc

Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)