Question 732612: A rectangular piece of metal is 10 in. longer than it is wide. Squares with sides 2 in. long are cut from the four corners, and the flaps are folded upward to form an open box. If the volume of the box is 832 in^3, what were the original dimensions of the piece of metal?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The original piece of metal measured  by by . .
THE FIFTH GRADER WAY TO THE SOLUTION:
The box will have a height of 2 inches.
Volume is area of the base times height, so for a volume of 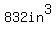 with a height of with a height of 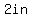 , the surface area of the base of the box must be , the surface area of the base of the box must be

The length and width of the base of the box will still be 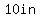 apart, just as the length and width of the rectangular piece of metal were, because the flaps are taking off the same amount from length and with, so the dimensions of the base of the box, in inches, must be two numbers, 10 units apart whose product is 416. apart, just as the length and width of the rectangular piece of metal were, because the flaps are taking off the same amount from length and with, so the dimensions of the base of the box, in inches, must be two numbers, 10 units apart whose product is 416.
Dividing 416 by 2 repeatedly the fifth grader finds that the factorization of 416 is

Length and width numbers must both be even because they differ by 10, so the fifth grader tries to pait the 13 with a 2, to split the factorization into two factors like this:

and happily finds out that those factors are
 and and  and those must be the dimensions of the bottom of the box, since and those must be the dimensions of the bottom of the box, since  . .
With 2 inch flaps on each side adding 4 inches the length and width of the original piece of metal were:
 and and 
THE ALGEBRA WAY:
 = width of metal piece (in inches) = width of metal piece (in inches)
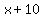 = length of metal piece (in inches) = length of metal piece (in inches)
With the flaps taking off 4 inches (2 on each side) from length and width, the base of the box will measure
 inches wide by inches wide by  inches long. inches long.
The surface area of the bottom of the box (in square inches will be
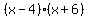
The volume of the box, in cubic inches, can be calculated by multiplying the surface area of the bottom times the 2-inch height of the box, so it is

Dividing both sides by 2 we get

There are many ways to solve the problem from this point on:
1) You could multiply to get a quadratic equation
 --> -->  --> --> 
and then solve the resulting quadratic equation by the method of your choice:
1A) Quadratic formula (painful, but effective):
 --> -->  --> -->  --> --> 
At this point you choose  only, only,
because the other choice gives you an unrealistic negative length.
 --> -->  --> --> 
1B) Completing the square (always effective, sometimes painful):
 --> -->  --> -->  or or
 --> -->  --> -->  and then and then
 --> -->  --> -->  --> -->  --> only --> only  --> -->  because because  <--> <--> does not make sense. does not make sense.
1C) Factoring (works in this case, but not always):
 --> -->  --> only --> only  --> -->  because because  <--> <--> does not make sense. does not make sense.
2) You could think like a fifth grader and decide that   work, so work, so  --> --> 
3) You could decide you want to do mental math and pick  midway between the 10-units-apart midway between the 10-units-apart  and and 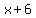 (their average, in other words). (their average, in other words).
With that (mental) substitution,  turns into turns into
 --> -->  --> -->  --> -->  --> --> 
and because  <-> <-> <--> <--> does not make sense does not make sense
 --> -->  --> --> 
|
|
|