Question 717520: when solving -x2+2x+1=y when x is -1, would it be -1 + -2 +1= y or 1 + -2 + 1=y?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your question, in simpler terms, is: What is  when x = -1? when x = -1?
The answer requires that we understand a fundamental fact about exponents: Exponents apply only to what is immediately in front of them. ("Immediately in front" means literally "the very first character to the left of"- If a digit (0-9) is immediately in front of the exponent, the exponent applies only to the number which that digit is the last/only digit. Important: If there is a "-" in front of this number, the exponent does not apply to it! For example:
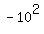 means -(10*10) which equals -100 (not (-10)(-10) which equals 100. means -(10*10) which equals -100 (not (-10)(-10) which equals 100. - If a variable is immediately in front of an exponent, the exponent applies only to that variable, not to any other variables or numbers which may precede that variable. For example,
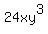 means 24*x*y*y*y. means 24*x*y*y*y. - If a end-of-a-group symbol (like "}" or "]" or "}") is immediately in front of an exponent, it applies to the entire grouped expression. For example,
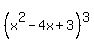 means means 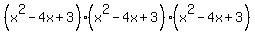 but but 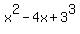 means just means just 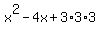
The way exponents work like this is another reason it is a good idea to use parentheses when making substitutions. If you substitute a -1 into  with parentheses you get: with parentheses you get:

Without the parentheses we would have:

Finally we'll answer your question, if you haven't figured it out already.  when x = -1: when x = -1:

|
|
|