Question 715455: Graph the function y<-3x^(2)+4x-5
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! The graph of the equation  is a parabola which opens downward. We will use the graph of this parabola as a guide to the graph of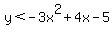 
The points on the parabola represent where the y is equal to 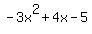 . Our inequality, however, does not have "or equal to", just "less than", so the points on this parabola will not be solutions to the inequality. For this reason, we draw the parabola as a "dotted" line. The "dotted" line means "not including these points". So go ahead and graph the parabola for using a dotted line, not a solid one.
Once that is done, we will figure out where the solutions to the inequality are. They will be either inside the dotted line of the parabola or outside the dotted line. There are two ways to figure this out:- The inequality says that y is less than 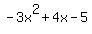. Since y is the variable that goes up and down on the graph and since we want y's that are less than the y's of the parabola, then the y's of the inequality will be down fron the parabola:
- Pick any point on the dotted line parabola.
- Go straight down from there.
- Wherever you end up will have a y-coordinate that is less than 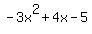. So this area, everything on this side of the dotted line, is the solution to the inequality
- Pick a specific point that is clearly inside (or outside) the dotted line parabola. (Make sure it is nowhere near the dotted line parabola.) And then see if the coordinates of that point fit the inequality (i.e. replace the x and y in 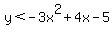with the coordinates and see if the statement is true or false. If it is true then that area is where the solutions are. If not, then the other side of the dotted line parabola is where the solutions are.
Once you figure out which side of the dotted line parabola has the solutions, then shade in that entire area. This shaded area is the graph of the solutions to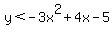
|
|
|
