Question 704143: Determine the equation of the axis of symmetry of a quadratic function that has zeros -3 and 5. I know the equation for axis of symmetry is x=-b/2a...but I don't know how to find those numbers with only having the zeros? Any help would be greatly appreciated:)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The axis of symmetry is vertical,
Being an axis of symmetry,
it must pass through the middle of any horizontal segment between two points in the graph of the quadratic function.
The mid-point between (-3,0) and (5,0) is (1,0) and is part of the vertical axis of symmetry you are looking for.
The coordinates of a midpoint can be easily calculated as the averages of the coordinates of the end points of the segment
 and and 
The equation of that vertical axis of symmetry is  . .
Another way:
A quadratic function with zeros at -3 and 5, must have for factors
 and and 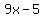
We can write it as
 --> -->  --> --> 
THere are infinte such quadratic functions, but all have the same axis of symmetry.
You would calculate it using 
as  --> --> 
EXTRA:
To find a polynomial function of degree  you need you need  points. points.
In particular, 2 points define a line (a linear function),
and 3 points define a parabola (a polynomial function of degree 2, also called a quadratic function).
|
|
|