Question 64540This question is from textbook glencoe algebra 2
: Bryan Starr is a 17 year old high school senior from Upper Arlington, Ohio, who started his own lawn service when he was 12. His business has grown substantially and he has been able to put away money for college, buy a truck, and invest in a new lawn equipment to keep up with the growing demand for his services. Suppose his weekly revenue R can be represented by the formula
R= -p[squared] + 50p-125, where p is the average price he charges for each lawn.
a) Sketch a graph of the related function. Explain why it behaves like it does, considering Bryan's business.
b) Explain how Bryan could earn $400 each week.
c) What price should he charge to earn the maximum revenue? What would be his revenue?
d) Use the discriminant to find if there is a price he could charge that would make his weekly revenue $600. Explain.
This question is from textbook glencoe algebra 2
Found 2 solutions by stanbon, josmiceli:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose his weekly revenue R can be represented by the formula
R= -p[squared] + 50p-125, where p is the average price he charges for each lawn.
a) Sketch a graph of the related function. Explain why it behaves like it does, considering Bryan's business.
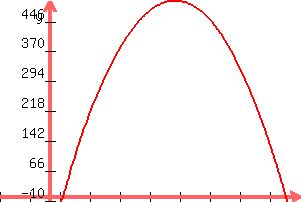
-----------------------
b) Explain how Bryan could earn $400 each week.
Revenue is $400 when price is $15 or when price is $35
----------------------------------
c) What price should he charge to earn the maximum revenue? What would be his revenue?
Revenue is at a maximum when p=-b/2a=-50/-2=$25; Revue is $500
----------------
d) Use the discriminant to find if there is a price he could charge that would make his weekly revenue $600.
600=-x^2+50x-125
-x^2+50x-725=0
discriminant=50^2-4*-1*-725; this result is negative meaning p is inot a
positive real number. Revenue could never be $600.
-----------
Cheers,
Stan H.
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|