Question 642151: x2-10x= ? find the number that should be added to each expression to make it a perfect square thanks for the help!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I can give you a recipe, but it is better to understand the rationale behind the procedure.
If you try to memorize a procedure, you may forget it, get confused, or remember it wrong.
I believe that if you understand why people do something a certain way, you will always remember just what you need to know to do it right every time. There's no need to memorize stuff in math.
THE RECIPE:
You need to look at the term in  . .
(In this case, it is 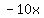 ). ).
Divide it by 2. (You get 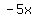 ). ).
Then divide that by the  that is squared in the first term, the that is squared in the first term, the  term. term.
(You get 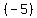 , which is an important part of the answer). , which is an important part of the answer).
Next, square that number.
(You get  , which is the other important part of the answer). , which is the other important part of the answer).
Your answer is 
Your teacher prefer to see it as

THE RATIONALE
The square of a binomial (represented by 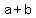 ) is given by ) is given by

Your  is is  , your , your 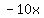 is is 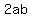 , ,
and you are trying to find  and and 
(Textbooks and teachers will also give you
 , but that is the same thing with , but that is the same thing with  ). ).
Those formulas (and algebra in general) look like Greek to many people.
I like to see it as pictures and as real life issues.
I read that formula as
The square of a binomial (sum) is the sum of two squares plus two rectangles.
Imagine that you are adding to a square patio, to make a larger square patio.
It would look like this:
 As you add As you add  to the length of your original blue to the length of your original blue  by by  patio, you are adding the two green patio, you are adding the two green  by by  rectangles on the sides, rectangles on the sides,
and the red  by by  square to fill the corner. square to fill the corner.
|
|
|