Question 638460: An envelope has an area of 80cm^2. If the length is 4cm longer than the width, use algebraic methods to find the dimensions of the envelope. (Round answer to 1 decimal place value).
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! The area of a rectangle is determined by finding the length times the width. Let's use L for length and W for Width and A for Area: A = L x W
We know the total area of the envelope is 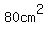 . In other words, . In other words,  . The question says the length is 4cm longer than the width. So, . The question says the length is 4cm longer than the width. So, 
To solve our problem, and since we know what L equals, in relation to W, and we know what A equals, we will replace L and A in our area formula:

Using the distributive property, we will multiply W by what is in the parenthesis:
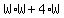 , which equals , which equals 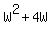
Now we have an equation that looks like the following:

If we subtract both sides of the equal sign by 80, we are left with a quadratic equation:

We cannot solve this by factoring, because there are no two numbers that can be multiplied by 80 that can also be added together to equal 4. So, we will use the quadratic formula to solve for W:
 = =
 = =

We can now reduce the square root down, because 16 x 21 = 336, and 16 is a perfect square. So, we are left with:

Since 2 is a factor of 4 and 2, we can divide each of our numbers (excluding what's inside the square root, by 2, leaving us with:

Since a rectangle cannot have any negative sides, we know that our width cannot equal 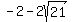 , because this equals a negative number. So, our width is , because this equals a negative number. So, our width is 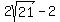
Since we know the length is 4 more than the width, to find the length, we will just add 4 to our width:
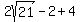 , which leaves us with , which leaves us with 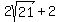 . .
We can validate our length and width by multiplying them together. If that answer equals 80, then we know our length and width are correct:
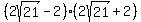 = =
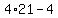 = =
 = =
80
So, are length and width are correct.
Final Answer:
 cm cm
 cm cm
|
|
|