Question 633640: I need help with a few problems that I have been working on but I can't seem to get exactly what it is I need, which is understanding how to work these problems and show my work. Please and thank you for any help you can offerme at this time.
Problem # 1: In this problem it asks to find the vertex, the line symmetry, and the maximum or minimum value of f(x). Graph the function. f(x)=1/3(x+6)^2+4.
Problem # 2: Find the variation constant and equation of variation where y varies directly as x and y=12 when x=2.
Problem #3: Rationalize the denominator. Assume that all expressions under radicals represent positive numbers. sq rt u-sq rt /sq rt u+sq rt v
Problem #4: Convert to decimal notation. 8.91*10^7
Problem #5: In a right triangle, find the length of the side not given. b=1, c=sq rt 10. The third length of the third side is?
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem # 1: In this problem it asks to find the vertex, the line symmetry, and the maximum or minimum value of f(x). Graph the function. f(x)=1/3(x+6)^2+4.
This is in standard form, y = a(x-h)^2 + k, where (h,k) is the vertex, and x = h is the LOS.
-----
The minimum is at the vertex, (h,k) = (-6,4).
==================================================
Problem # 2: Find the variation constant and equation of variation where y varies directly as x and y=12 when x=2.
y = kx
12 = 2k
k = 6
===================
Problem #3: Rationalize the denominator. Assume that all expressions under radicals represent positive numbers. sq rt u-sq rt /sq rt u+sq rt v
Multiply NUM and DEN by the conjugate of the DEN, 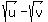
----------
The NUM has a missing term, probably is sqrt(v)
--> 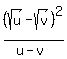
You can expand the NUM, or not.
--------------------------------
Problem #4: Convert to decimal notation. 8.91*10^7
Move the DP 7 places to the right, adding zeroes as needed.
= 89100000
===============
Problem #5: In a right triangle, find the length of the side not given. b=1, c=sq rt 10. The third length of the third side is?
If c is the hypotenuse, then

a = 3
|
|
|