Question 633226: 4x^2-4sq.root3x+3=0
sq.root2x^2-3x+sq.root2=0
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Those equations may be scary because of the square roots, but they are just quadratic equations. All that the square roots can do is scare you and cause you to make mistakes in the calculations.
I'll show you several ways to solve them. You can chose your way to solve each one.

SMART FACTORING:
 is a square. is a square.
I would say that  is another square. is another square.
Is 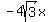 twice the product of twice the product of  and and  ? ?
Yes,  . .
Then,  is the square of a binomial. is the square of a binomial.

The equation can be written as
 --> -->  --> --> 
COMPLETING THE SQUARE:
 --> -->  --> --> 
Adding  (the square of -sqrt(3)/2) to both sides we form the square of (the square of -sqrt(3)/2) to both sides we form the square of 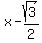 on the left side: on the left side:
 --> -->  --> -->  --> -->  --> --> 
USING THE QUADRATIC FORMULA:
For the generic quadratic equation  the solution(s) is/are the solution(s) is/are
 (if what's under the square root is not negative) (if what's under the square root is not negative)
In the case of  , ,  , ,  , and , and 
Substituting:
 --> --> 
 --> --> 
 --> --> 
 --> -->  --> --> 

USING THE QUADRATIC FORMULA:
 , ,  , and , and 
 --> -->
 --> --> --> -->
The two solutions are  and and 
Let's multiply numerator and denominator times 
because teachers do not like square roots in denominators
 --> --> --> --> and and  --> --> --> --> --> -->
COMPLETING THE SQUARE:
I would like to make the equation a little simpler and easier to work with.
 --> -->  --> --> 
 --> -->  (dividing both sides of the equation by 2) (dividing both sides of the equation by 2)
 --> -->
 --> --> --> -->
 --> -->
The two solutions would come from  and and 
 --> --> --> --> --> --> --> -->
 --> --> --> --> --> --> --> -->
FACTORING:
Starting from the simpler 
I would look for two numbers whose product is 1 and whose sum is 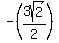 . .
They must be both negative and there is a  in there somewhere. in there somewhere.
Since the product is 1, one number is the reciprocal of the other, like  and and  . .
Trying  and and 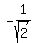 , I find that those numbers work , I find that those numbers work
 , ,
The sum is:

The product is

So the factoring gives me

meaning that thw equation can be written as
 and the solutions are and the solutions are
 and and 
|
|
|