Question 633223: Aki's bicycle designs has determined that when x hundred bicycles are built, the average cost per bicycle is given by c(x)=0.2x²-1.3x+8.181, where c(x) is in hundreds of dollars.
The shop should build_____bicycles.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a quadratic function. is a quadratic function.
As a quadratic function with a positive coefficient for the term in  , ,
it goes through a minimum.
Quadratic functions have the general form

They graph as parabolas,
and have a minimum or maximum at  . .
In the case of  , there is a , there is a
minimum at  --> -->  --> --> 
So the cost per bicycle is minimum when 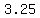 hundred bicycles are built. hundred bicycles are built.
That is 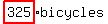
ABOUT QUADRATIC FUNCTIONS:
For a quadratic function,  , ,
when the leading coefficient,  , is positive, , is positive,
the function grows without bounds as  increases on both ends (positive and negative), increases on both ends (positive and negative),
as the  term overwhelms whatever value the rest of the polynomial could take. term overwhelms whatever value the rest of the polynomial could take.
As a consequence the function looks like a smile, with a minimum in the middle:

If  the shape of the graph is flipped and the function has a maximum: the shape of the graph is flipped and the function has a maximum:

The maximum or minimum is the vertex of the parabola.
The function can be transformed algebraically from  to to

which shows that the extreme value (maximum or minimum) occurs when
 , when , when 
and the line represented by  is the axis of symmetry of the parabola that is the graph of the function. is the axis of symmetry of the parabola that is the graph of the function.
If the expression reminds you of the quadratic formula, it is no coincidence.
The quadratic formula comes from the same
 making making  . .
|
|
|