Question 631098: I have tried and tried on this problem and just cant get it right. I even had a tutor online help me and they got it wrong too... this is the problem ...
Solve the system of equations. Round approximate values to the nearest ten-thousandth.
y = log2x
y = x−5
Found 3 solutions by richwmiller, solver91311, KMST:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Maybe something in the problem got "lost in translation."
For example, I wonder if you meant
 for the first function, for the first function,
or maybe it was 
The answer would depend on what that first function is.
In either of those cases, the log function and the y=x-5 function graphs will cross at two points, like this:
 , so you would have 2 solutions (which I will show you further down). , so you would have 2 solutions (which I will show you further down).
It could also be that the problem is neither of those, and something in the problem is irretrievably "lost in translation."
It could also be that the "officially correct answer" that you were given is wrong, or that it needs to be entered in a specific format. After seeing my youngest child through (online) high school courses, I would not be surprised. Sometimes the official answer was wrong, and sometimes the computer would accept only (8,3), but not (8, 3) or the other way around.
If it is  , ,
for  , ,  and and  . .
So 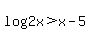 but they are very close. but they are very close.
For a smaller x,  , ,  and and  , with , with 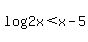 but they and very close. but they and very close.
That means that the answer for x must be a number in between, that I would round to 0.00001 if I was allowed, but it rounds to 0.0000 when rounded to the nearest ten-thousandth.
The answer for y is -5.0000 when rounded to the nearest ten-thousandth, because for  , for , for  , and for everything in between, the values of , and for everything in between, the values of 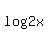 and and  rounds to -5.0000. rounds to -5.0000.
That solution would be expressed as (0.0000, -5.0000).
On the other end, I found that  seemed to be the closest I could get, with seemed to be the closest I could get, with
 and and
 =1.0853 (rounded). =1.0853 (rounded).
That would give you the (x, y) pair (6.0853, 1.0853).
If it was  , ,  with with  or (3, 2) is a nice exact answer. Another solution is or (3, 2) is a nice exact answer. Another solution is  with with  which rounded gives you the pair (0.0319, -4.9681). which rounded gives you the pair (0.0319, -4.9681).
|
|
|