Question 625213: I need help, I am stuck on this word problem from Quadratic Equations:
The number of tickets sold each day for an upcoming performance of Handel's Messiah is given by N(x)=-0.5x^2+11x+15, where x is the number of days since teh concert was first announced. When will the daily ticket sales peak and how many tickets will be sold that day?
Found 2 solutions by lwsshak3, jsmallt9:
Answer by lwsshak3(11628)   (Show Source):
You can put this solution on YOUR website! I need help, I am stuck on this word problem from Quadratic Equations:
The number of tickets sold each day for an upcoming performance of Handel's Messiah is given by N(x)=-0.5x^2+11x+15, where x is the number of days since teh concert was first announced. When will the daily ticket sales peak and how many tickets will be sold that day?
**
N(x)=-0.5x^2+11x+15
This equation is that of a parabola that opens downwards (negative lead coefficient)
Parabola has a maximum
Its form of equation:y= -A(x-h)^2+k, (h,k)=(x,y) coordinates of the vertex.
N(x)=-0.5x^2+11x+15
to find vertex, complete the square:
N(x)=-0.5(x^2-22x+121)+15+60.5
N(x)=-0.5(x-11)^2+75.5
vertex: (11,75.5)
When daily ticket sales will peak: 11 days since concert was announced
Tickets sold that day=75
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! First of all, keep in mind that function notation [N(x), f(x), g(x), etc.] is just a glorified y. So we can think of
as
Looking at N(x) this way may help you recognize that the graph of this function, because of the squared term, is going to be a parabola. And since it is x squared and not y squared, the parabola is vertically-oriented. And with a negative coefficient in front of the squared term, this parabola will open downward. If we picture such a parabola, we will see that the vertex of this parabola will be the highest point on the graph. The x coordinate of this highest point represents the day of the highest ticket sales and the y coordinate is the number of tickets sold that day. Our task, then, is to find the vertex of this parabola.
One way to find the vertex is to transform the equation into vertex form:
Another way to do this requires that you remember this fact: For the equation of a parabola in standard form ( ), the x coordinate of the vertex will be -b/2a. If you can remember this, this is the easy way to find a vertex.
Our equation is already in standard form with a "b" of 11 and an "a" of -0.5. So the x coordinate of the vertex will be:
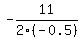
which simplifies as follows:
11
So the x coordinate of the vertex, which is the day of the highest ticket sales, is 11. To find how many tickets were sold on that day we just find N(11):
which simplifies as follows:
Note that we did not get a whole number. These modeling equations are not perfect models. After all, there are many x and y coordinates on this graph that are not whole numbers. So the best we can do with an imperfect model is to take the results "with a grain of salt". We have to interpret the results in the context of reality. Fractions of tickets are not sold. So we have to look at our answer of 76.5 as being a 76 or 77.
|
|
|
