SOLUTION: I need to simplify this expression to the simplest form. {{{((x^2-9x+20)/(2x^2-7x-15))((2x^2-x-6)/(8+2x-x^2))}}}

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: I need to simplify this expression to the simplest form. {{{((x^2-9x+20)/(2x^2-7x-15))((2x^2-x-6)/(8+2x-x^2))}}}      Log On


   

Question 623787: I need to simplify this expression to the simplest form.
%28%28x%5E2-9x%2B20%29%2F%282x%5E2-7x-15%29%29%28%282x%5E2-x-6%29%2F%288%2B2x-x%5E2%29%29
Answer by math-vortex(648) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, there---

Let's begin by trying to factor each of these trinomials. Typically, in textbook problems you 
will discover some common factors that you can then cancel out.

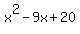x%5E2-9x%2B20

We need two numbers whose product is 20 and whose sum is -9; the numbers are -4 and -5.
x%5E2-9x%2B20=%28x-4%29%28x-5%29

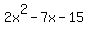2x%5E2-7x-15
The leading coefficient is 2 so we have an extra step to find the factors. 2x^2 factors as (x)(2x) 
and -15 factors as (-3)(5) or (3)(-5). The numbers are -5 and 3 because (2x)(-5)-(x)(3)=-7x.
2x%5E2-7x-15=%282x%2B3%29%28x-5%29

Using similar reasoning,
2x%5E2-x-6=%282x%2B3%29%28x-2%29

8%2B2x-x%5E2=%28-1%29%28x%5E2-2x-8%29=%28-1%29%28x-4%29%28x%2B2%29

Therefore,


Notice that (x-4), (2x+3), and (x-2) appear in the numerator and the denominator. We can 
"cancel these out" because a number divided by itself always equals 1. Any number multiply 
by 1 equals the same number.

Now we have 


Simplifying, we move the -1 outside the fraction.


Please email me if you have questions about this solution. I'll be happy to help you sort it out.

Ms.Figgy
math.in.the.vortex@gmail.com