Question 621373: what is the equation required to create a simple wine glass in a graph and how can we find its volume?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Since you placed that question under "Quadratic Equation", I assume the expected profile is a parabola, the graph of a quadratic function. I inspected all the wine glasses in my china cabinet and in my wine cupboard and concluded that a paraboloid is not the shape of a wine glass. The mouth of the glass is never the widest part. Wine glasses can be shaped like truncated ellipsoids (white wine glasses) or have a truncated egg shape (with the tip cut off). The bulb of wine glasses is not shaped like a paraboloid, but I guess a paraboloid is the simple shape envisioned. (I would suggest a truncated ellipsoid, but you may not have studied ellipses yet).
I also assume that you are in a Calculus class and were taught how to use integration to find the volume of a solid of revolution.
If the height above the bottom of the bulb is  and the cross-section radius is  , the shape of a paraboloid wine glass bulb would given by
 <--> 
A cross section of the glass is a circle with area  ,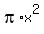
and since , that cross section area would be 
If the height of the bulb (vertical distance from the rim to the bottom of the bulb) is H, the volume could be calculated as
If you use centimeters, then you would get the volume in cubic centimeters, which are essentially the same as milliliters.
I would chose something close to 6-8 cm for the diameter at the top, and 10 cm for the height (H) of the wine glass bulb.
With a paraboloid shape, and an 8-cm top diameter, you have x=4 and h=10 at the rim, so
 -->  .
In that case
 = about 196 mL
|
|
|
