SOLUTION: The length of a rectangle is 2 times its width. The area of the rectangle is 72 square inches. Find the dimensions of the rectangle. How would I solve this by factoring

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: The length of a rectangle is 2 times its width. The area of the rectangle is 72 square inches. Find the dimensions of the rectangle. How would I solve this by factoring      Log On


   

Question 610508: The length of a rectangle is 2 times its width. The area of the rectangle is 72
square inches. Find the dimensions of the rectangle.
How would I solve this by factoring?
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
First you need an equation. The factoring comes later.

The equation we will use is the equation for area of a rectangle:
A = l*w
We know the area. We do not know the length or width so we will need to write expressions for them. In general, it is helpful if you make the variable represent the lowest unknown number. In this case it would be the width. So we will have...
x = width of the rectangle
Since the length is 2 times the width and since the width is x, this makes...
2*x = length of the rectangle.

Now, in the equation for area, we substitute in for A, l and w:
(72) = (2*x)*(x)

Now that we have an equation we can start solving the problem. As usual, you start by simplifying each side:
72+=+2x%5E2
This is a quadratic equation (because of the x%5E2 term). So we want one side to be zero. Subtractin 72 from each side we get:
0+=+2x%5E2+-+72
Next we factor (or use the Quadratic Formula). You were told to factor so that is what we will do. When factoring, alwyas start with the GCF. Here the GCF is 2:
0+=+2%28x%5E2+-+36%29
Next we want to factor 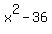x%5E2-36. Since 36+=+6%5E2 this is a difference of squares. A difference of squares factors according to the pattern: a%5E2-b%5E2+=+%28a%2Bb%29%28a-b%29. Using this pattern to factor x%5E2+-+36 we get:
0+=+2%28x%2B6%29%28x-6%29
Now that the right side is fully factored, we use the Zero Product property which tells us that any product can zero only if one (or more) of the factors is zero. The factor of 2 cannot be zero but the other two factors could. So:
x+6 = 0 or x-6 = 0
Solving each of these we get:
x = -6 or x = 6

Remembering that x represents the width of the rectangle and knowing that widths cannot be negative, we discard the negative solution. So the width of the rectangle is 6. For the length we have to remember that it was 2*x. So the length is 2*6 or 12. (Note: It is a good habit to write down what you variable represents, like we did for the width above, and to write down other expressions you may have used, like we did for the length above. This way you can just look back to see how to user the value you found for "x" to determine what the answer(s) are to the problem.