Question 610240: 3x2 + 7x > -12
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 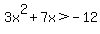
Like quadratic equations, you want one side to be zero and then factor the other side. Adding 12 to each side we get:
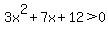
Then we factor. But this won't factor!
We can use the Quadratic Formula to tell us something helpful:

Simplifying:



At this point, with the negative in the square root, we can stop. The formula is trying to tell us x value(s) that make 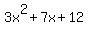 equal to zero. Since we cannot have a negative inside a square root, this tells us that equal to zero. Since we cannot have a negative inside a square root, this tells us that 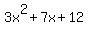 is never equal to zero. is never equal to zero.
If 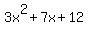 is never equal to zero, it must always be positive or always be negative. We can quickly see that when x = 0, is never equal to zero, it must always be positive or always be negative. We can quickly see that when x = 0, 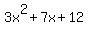 will be a 12. 12 is positive. Since will be a 12. 12 is positive. Since 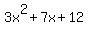 is always positive or negative and since we have found a case where it is positive, is always positive or negative and since we have found a case where it is positive, 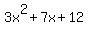 must always be positive. So the solution to must always be positive. So the solution to
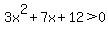
which says that 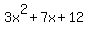 is positive, is: is positive, is:
All real numbers. In other words, no matter what number you use for x, 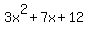 will work out to be positive. will work out to be positive.
|
|
|