SOLUTION: Hello Math peoples, I would really appreciate some help on the forming and solving a quadratic equation. THe Question is : " Subtracting a squared number from 68 gives the s

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Hello Math peoples, I would really appreciate some help on the forming and solving a quadratic equation. THe Question is : " Subtracting a squared number from 68 gives the s      Log On


   

Question 606551: Hello Math peoples,
I would really appreciate some help on the forming and solving a quadratic equation.
THe Question is : " Subtracting a squared number from 68 gives the same result as doubling the number"
So I endeavoured to solve and got 68-x^2=2x
-x^2-2x+68=0
Am I forming the correct equation ?
Many thanks

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You are correct.
"Subtracting a squared number from 68" translates as 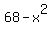68-x%5E2 where x is the mystery number, and "doubling the number" would be 2x, just as you wrote.
You could also write your quadratic equation as
x%5E2%2B2x-68=0 , or even as
x%5E2%2B2x=68 (equivalent equations).

COMPLETING THE SQUARE:
Since x%5E2%2B2x reminds me of x%5E2%2B2x%2B1=%28x%2B1%29%5E2, I would be tempted to "complete the square" by just adding 1 to each side of the equal sign in that last equation.
x%5E2%2B2x=68 --> x%5E2%2B2x%2B1=68%2B1 --> %28x%2B1%29%5E2=69
The solutions would be x%2B1=sqrt%2869%29 and --> x%2B1=-sqrt%2869%29
Then we could subtract 1 from each side of the equal sign in the equations above to get
x=sqrt%2869%29-1 and --> x=-sqrt%2869%29-1 which can be summarized as
highlight%28x=-1+%2B-+sqrt%2869%29%29

USING THE QUADRATIC FORMULA:
The other option is using the quadratic formula. Any equation of the form
ax%5E2%2Bbx%2Bc=0 has as solutions x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+.
That formula is called the quadratic formula.
From the values for the coefficient (a, b, and c) in any quadratic equation, you can find the solutions using that formula
If 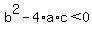b%5E2-4%2Aa%2Ac%3C0 the solutions are not real numbers, so if the only numbers you know are real numbers, then you say there are no solutions.
(By the way, the expression b%5E2-4%2Aa%2Ac is called the discriminant).
Plugging those values into the quadratic formula, any computer can solve a quadratic equation.
(Humans have more trouble because they tend to make mistakes in their calculations).
To apply the quadratic formula, if you start with -x%5E2-2x%2B68=0 you have
a=-1, b=-2 and c=68.
Plugging those values into the quadratic formula, you have
x+=+%28-%28-2%29+%2B-+sqrt%28+%28-2%29%5E2-4%2A%28-1%29%2A68+%29%29%2F%282%2A%28-1%29%29+ --> x=%282%2B-+sqrt%284%2B272%29%29%2F%28-2%29 --> x=%282+%2B-+sqrt%28276%29%29%2F%28-2%29 --> x=%282+%2B-+sqrt%284%2A69%29%29%2F%28-2%29 --> x=%282+%2B-+2%2Asqrt%2869%29%29%2F%28-2%29 --> x=2%2A%281+%2B-+sqrt%2869%29%29%2F%28-2%29 --> x=%28-1%29%2A%281+%2B-+sqrt%2869%29%29 --> x=-1+%2B-+sqrt%2869%29
(I feel tempted to write the plus sign on the bottom in
x=-1+%2B-+sqrt%2869%29 above,
to show that it was on the top before multiplying times (-1), but the order does not matter, and the symbol I can write has the plus on top).