Question 604247: Use the discriminant to determine the number of real solutions for the equation 8z^2-2z+6=0
a. 0
b. 1
c. 2
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! For a quadratic equation of the standard form:
.

.
in which "a" is the multiplier of the z^2, "b" is the multiplier of the z, and c is a constant, the discriminant is given by:
.
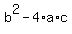
.
The quadratic equation you are given in this problem is:
.

.
Let's now compare this term-by-term with the standard form. The multiplier of the z squared is 8. Therefore, we can say "a" equals 8. The multiplier of the z is -2. So we can say that "b" is -2. And finally the constant is +6 and we know that c equals +6.
.
Let's substitute these numeric values for their corresponding values in the discriminant. When we do that the discriminant becomes:
.
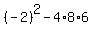
.
Squaring the -2 results in 4, and multiplying out the second term gives -192. So the discriminant becomes:
.
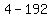
.
and after doing the subtraction, we find that the value of the discriminant is -188.
.
What does this tell you about the solutions to the equation you were given? The rules for the discriminant say:
.
If the discriminant is a positive value, the solutions to the quadratic equation will be two real roots that are unequal. (The graph of the quadratic function will be a parabola that crosses the horizontal axis at two separate points.)
.
If the discriminant equals zero, the solutions to the quadratic equation will be two real and equal roots. (The graph of the quadratic function will be a parabola whose vertex touches the horizontal axis at just a single point.)
.
If the discriminant is a negative value, the solutions to the quadratic equation will be two roots that are imaginary. (The graph of the quadratic function will be a parabola that does not cross or touch the horizontal axis.)
.
Since the discriminant for this problem was negative, this means that the solution to this problem is a pair of imaginary roots. So the answer to this problem is that there are zero real roots for the equation given in this problem. (Answer "a" from the list of potential answers is the correct one for this problem.)
.
I hope this helps you to understand the usefulness of the discriminant in determining the form of the potential answers for quadratic equations.
.
|
|
|