Question 597910: in the formula shown here:
http://www.algebra.com/cgi-bin/plot-formula.mpl?expression=x+=+%28-b+%2B-+sqrt%28+d+%29%29%2F2a&x=0003
(paste in the browser)
(note: this is the quadratic formula)
I do not understand what the little box means in the equation. (in between the 2 and a.) Please explain! and it will also help to explain the whole thing, as I don't really understand all the signs, as I haven't learnt any of it before...thanks in advance:)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Depending on how much you've learned of algebra so far, this could be a little confusing or very confusing, but here it goes.
THE SYMBOLS FOR MULTIPLICATION:
At the bottom of the formula, between the 2 and the a , there is symbol called a middle dot.
That is a symbol used in algebra to mean multiplied by. The expression 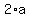 means 2 times a. means 2 times a.
In algebra, the letter x is used a lot. The old X multiplication sign that is used in third grade looks too much like the letter x. That old X symbol could cause confusion, so it is not used.
Sometimes a middle dot is used to indicate multiplication, as in
 or or 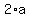 . .
If there is no room for confusion, the middle dot can be skipped, so we are allowed to write  instead of instead of 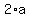 . .
To make matters a little more confusing, the asterisk is used as a middle dot when typing a middle dot symbol is difficult or impossible. So you may see 2*a instead of  or or 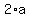 . .
THE QUADRATIC FORMULA:
The quadratic formula is used to find solutions to quadratic equations like
 . .
All quadratic equations can be represented with the general equation
 where a, b, and c represent the numbers in the equation. where a, b, and c represent the numbers in the equation.
For  , a is 15, b is -14, and c is -8. , a is 15, b is -14, and c is -8.
Some quadratic equations have one or two real solutions. For other quadratic equations, there is no real number that could be a solution. It all depends on the value of an expression called the discriminant. In the formula you are asking about, the letter d represents the discriminant.
The discriminant is the expression
 The 4, a, and c are multiplied together. The 4, a, and c are multiplied together.
For  , the discriminant is , the discriminant is

If the discriminant is positive (as for the equation  , with , with  for a discriminant), there are two distinct (meaning different) real solutions. They can be calculated using the formula for a discriminant), there are two distinct (meaning different) real solutions. They can be calculated using the formula

For  , it would be , it would be

One solution is
 . .
The other is
 . .
|
|
|