Question 578005: Solve.
(x+16)(x-10)(x+7)>0
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Each of the factors has a zero. Each factor is equal to zero for that x value; it's positive for greater x values and negative for lesser x values.
The zeros, where one factor is zero, and therefore the whole product expression is zero are:
 , ,  , and , and 
For 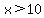 , all 3 factors and the product are positive , all 3 factors and the product are positive 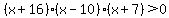
As we move across each zero, one of the factors changes sign, and so does the product.
For 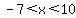 , , 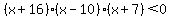
For 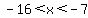 , , 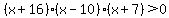
For  , , 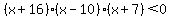
So the solutions are 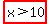 and and 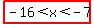 . .
|
|
|