Question 560286: what is the two numbers that multiplies to get 4 and adds to make 6
Please help
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's call one of the unknown numbers x and the other unknown number y.
.
The problem tells you that if you multiply the two unknown numbers you get an answer of 4. Let's do that in equation form. The left side of the equation will be the product of x and y and the right side of the equation will be 4. So:
.
 <---- our first equation <---- our first equation
.
Next the problem tells you that if you add the two unknown numbers, the answer is 6. In equation form this is:
.
 <---- our second equation <---- our second equation
.
To solve for two unknowns you must have at least two independent equations involving those unknowns. We have our two independent equations so, if there is a solution, we should be able to find it for the two unknowns, x and y.
.
We will use the substitution method for solving this problem. We will begin by solving the second equation for y. Then what we will do is substitute that value for y into the first equation and solve it for x. Here's what we will do:
.
Start with our second equation:
.

.
Solve it for y by subtracting x from both sides to get:
.

.
Since the right side of this equation is equal to y, we can go to our first equation and substitute 6 - x for y in it to get:
.

.
This is now a single equation with only 1 unknown. If it has a solution, we should be able to solve it for that one unknown. Let's try.
.
First do the distributed multiplication on the left side by multiplying x times each of the terms in the parentheses to change the equation to:
.

.
We are now see that this is a quadratic equation because it has a squared term. Let's try to get it into the standard quadratic form, which has all the terms in descending powers of x on the left side and is equal to zero on the right side.
.
Begin by subtracting 4 from both sides to get:
.

.
Rearrange the terms on the left side so they are in descending powers of x as follows:
.

.
We wouldn't have to do this, but let's make the first term on the left side be positive by multiplying both sides (all terms) by -1. This will change the equation to:
.

.
Note that this is in the standard quadratic form of:
.

.
and by comparing terms we can see that a (which is the multiplier of the squared term) is 1, b (the multiplier of the x term) is -6, and c (the constant) is +4.
.
The quadratic formula says that for a standard quadratic form, the solution is given by:
.

.
So all we have to do to solve for x is to substitute the values for a, b, and c that we identified above (a = 1, b = -6, c = 4). When we substitute these values into the solution equation we get:
.

.
Now notice that the first term in the numerator is -(-6). We can remove the parentheses if we just change the sign of the term within. So -(-6) becomes just +6. Next, inside the radical we square the -6 to get + 36. Then inside the radical we multiply -4*1*4 to get -16. And finally in the denominator we multiply the 2*1 to get just 2. With all these changes the solution for x becomes:
.

.
The subtraction of 36 - 16 inside the radical results in 20 as shown below:
.

.
Now let's reduce the radical by simplifying it. Start with:
.
 and recognize that this is equal to and recognize that this is equal to 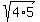
.
By the rules for radicals this can be split into two separate radicals:
.

.
But the square root of 4 is 2. Substitute that value for the square root of 4 and we have the form:
.

.
Now return to our equation for x which was:
.

.
and substitute 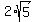 for for  to get: to get:
.

.
Finally, divide the two terms in the numerator by the 2 in the denominator, and the answer for x becomes:
.

.
Note that there are two possible answers for x.
.
One is that  and the other is and the other is 
.
From way earlier in this problem we found that  . We can now use this to find the two corresponding values for y. . We can now use this to find the two corresponding values for y.
.
When  then we substitute that value for x into the equation for y to get: then we substitute that value for x into the equation for y to get:
.

.
and when we remove the parentheses this becomes:
.

.
which by subtracting the 3 from the 6 arrives at the answer:
.

.
We can do a similar procedure to find y when  and we will find that for that with that value of x the corresponding value of y is: and we will find that for that with that value of x the corresponding value of y is:
.

.
So we have two possible sets of answers:
.
Set 1 is  and and 
.
and the other is:
.
Set 2 is  and and 
.
Look closely at these two sets. We can combine these two answers by summarizing them as follows:
.
In either case:
.
One of the numbers is 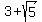 and the other is and the other is 
.
That's the answer we were to find.
.
Check by adding the two numbers:
.
The +square root of 5 cancels with the -square root of 5 and you are left with 3 + 3 which equals 6 just as the problem requires.
.
Then multiply the two numbers. You can use the factoring rule:
.

.
In this problem a = 3 and b = square root of 5. So the multiplication results in:
.

.
and since 9 - 5 = 4, the multiplication of the two terms does give the required answer of 4.
.
We have met the two conditions (product = 4 and sum = 6). So our answer is correct.
.
I hope this helps you to identify, understand, and get through the parts of the problem where you were having trouble.
.
|
|
|