Question 493948: Hi. I'm trying to do my algebra 2 GT homework and I have no idea how to do it by hand. I know how to plug it into the calculator and get the graph and answer, but I don't remember how to do so by hand. The problem says to "Graph the function. If a > 0 find the minimum value. If a < 0 find the maximum value. The function is y= 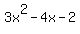 . THANK YOU!! . THANK YOU!!
Found 2 solutions by Theo, lwsshak3:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the function is 3x^2 - 4x - 2
set it equal to 0 to put it in standard form of:
ax^2 + bx + c = 0
this makes:
a = 3
b = -4
c = -2
since a is positive, the max/min point will be a min point.
the formula to find the max/min point is:
x = -b/2a
this becomes:
x = -(-4)/(2*3) = 4/6 = 2/3
when x = (2/3), y = 3*(2/3)^2 - 4*(2/3) - 2 which becomes:
3 * 4/9 - 8/3 - 2 which becomes:
12/9 - 8/3 - 2 which becomes:
12/9 - 24/9 - 18/9 which becomes:
(12 - 24 - 18) / 9 which becomes:
-30 / 9 which becomes -3.33333
you have x = 2/3 and y = -3.333333
that's the min point.
a graph of your equation looks like this:

i placed a horizontal line at y = -3.333333 and a vertical line at x = 2/3 in order to show you where the min/max point is.
once again, this is a min point because a is positive.
if a was negative, the graph would be pointing up rather than down.
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi. I'm trying to do my algebra 2 GT homework and I have no idea how to do it by hand. I know how to plug it into the calculator and get the graph and answer, but I don't remember how to do so by hand. The problem says to "Graph the function. If a > 0 find the minimum value. If a < 0 find the maximum value. The function is y=3x^2 - 4x - 2
**
What you have here is a parabola whose standard form of an equation is:
y=a(x-h)^2+k, with (h,k) being the (x,y) coordinates of the vertex.
If a>0, the parabola opens upwards and you have a minimum.
If a<0, the parabola opens downwards and you have a maximum.
..
For given function:
y=3x^2 - 4x - 2
Complete the square
y=3(x^2-4x/3+16/36)-2-4/3
y=3(x-4/6)^2-10/3
vertex(2/3,-10/3)
ans:
since a=3>0
minimum value=-10/3
..
The graph below will help you to graph the function by hand. In addition to the vertex, you can easily get another point by setting x=0. F(0)=-2, the y-intercept. Also, remember the curve is symmetrical about the axis of symmetry, x=4.
..

|
|
|