Question 486733: to factor an equation of to forrm 24^2p-55p-24=0, find a pair of integers whose product is AC and addds up to B
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
factor an equation of to form  , ,
 .......replace .......replace 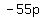 with the with the 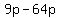
 .....group .....group



find a pair of integers whose product is  and adds up to and adds up to 
"Each of the trinomials is the form  " "
In this example,  , ,  , and , and  . We must find two integers whose product is . We must find two integers whose product is 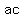 , or , or 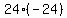 , and whose sum is , and whose sum is  . .
If the problem is too difficult to yield readily to inspection, we can find the prime factors of |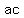 , or , or  and divide them into two piles. The prime factors of and divide them into two piles. The prime factors of  are are
2*2*2*2*2*2*3*3=2^6 * 3^2
which can be found easily by factoring |a| and |c| separately and combining the result.
letís try these:2^6 * 3^2


This adds to  , which has an absolute value greater than the required , which has an absolute value greater than the required  . .
letís try these:2^5(2 * 3^2)


letís try these:2^4(2^2 * 3^2)


letís try these:2^3(2^3 * 3^2)


letís try these:2^2*3(2^4 * 3)


letís try these:2*3(2^5 * 3)


Therefore, no pair of integers can satisfy the necessary requirements.
|
|
|