Question 475466: Can you please help me solve this word problem involving quadratic equations, I am lost and can't figure out where to start.
The function D(x) models the cumulative number of deaths from a disease x years after 1984, estimate the year when there were 100,000 deaths.
D(x) =2285x^2 + 5583x + 5540.
There were approximatley 100,000 in the year __________________
(round to the nearest year)
Your help will be appreciated!
Thanks Abby
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation is D(x) = 2285x^2 + 5583x + 5540
if you graph the equation, just replace D(x) with y and you have the equation that is ready for graphing.
that equation is y = 2285x^2 + 5583x + 5540
it looks like this:

from the graph, it looks like the cumulative number of deaths will reach 100,000 somewhere around the 5th year.
the formula to find that would be the formula you were given, but replacing D(x) with 100,000l, because, when the cumulative deaths reach 100,000, this means that D(x) = 100,000
The equation becomes:
100,000 = 2285x^2 + 5583x + 5540
subtract 100,000 from both sides of this equation to get:
2285x^2 + 5583x + 5540 - 100,000 = 0
combine like terms to get:
2285x^2 + 5583x - 94460 = 0
this is a quadratic equation that needs to be solved to give you your answer.
solve using the quadratic formula.
that formula is:
x = 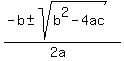
a = 2285
b = 5583
c = -94460
-b = -5583
b^2 = 31169889
4ac = -863364400
b^2 - 4ac = 894534289
sqrt(b^2-4ac) = 29908.76609
2a = 4570
x = 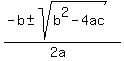 becomes: becomes:
x = 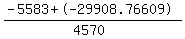
this gets you:
x = 5.322924746
or:
x = -7.766250785
Since x can only be positive, this means that x can only be equal to 5.322924746.
replacing x in the equation with 5.322924746 gets you:
D(x) = 2285x^2 + 5583x + 5540 becomes:
D(5.322924746) = 100,000
the graph and the equations check out ok so that's your answer.
The cumulative number of deaths from a disease will reach 100,000 5.322924746 years after 1984.
The fact that you are dealing with a quadratic equation might have thrown you off.
That starts off high and drops to a minimum value and then ends up high.
If we just extend the graph a little more to the left, you will see that better.

While that is a graph of a quadratic equation, and the equation starts off high and then drops to a minimum value and then goes up again, the only values of y in that equation are when x is greater than 0.
Look at the graph and you will see that the graph is rising from x = 0 and up.
Furthermore, you should see that y = 5540 when x is equal to 0.
That is the number of deaths that occurred in 1984.
x = 0 represents 1984.
x = 1 represents 1985.
etc.
You needed the quadratic formula to solve this problem.
With those large numbers, it was a little clumsy, but it worked fine.
you needed to start off with setting the equation equal to 100,000 as we did early on.
you need to then transform that equation into the standard form of a quadratic equation which we did by subtracting 100,000 from both sides of the equation.
once you got it into the standard form, it was simply the application of the quadratic formula to get the roots.
Here's a good reference on solving quadratic equations to find the roots.
It discusses the 3 main methods:
The quadratic formula method is near the bottom.
It's all good information, but just pick out what you need for now.
http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut17_quad.htm
|
|
|