Question 4403: The problem is : 2 positive numbers that differ by 7 whose product is 1 I have not been able to come up with an answer.
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = first number
y = second number
Write two equations based upon the first two sentences.
x-y = 7
xy = 1
Solve for x in the first equation by adding +y to each side.
x-y = 7
x-y+y= 7 + y
x = 7+y
Substitute x = 7+y into the second equation for x:
xy = 1
(7+y)y = 1
Next use the distributive property, and since a quadratic equation results, set it equal to zero.


This obviously does not factor, which may be why you had a problem with it. There are no whole number solutions that work!! Use the quadratic formula to solve it:
 , where a= 1, b=7, c=-1 , where a= 1, b=7, c=-1



It appears that there are two solutions
 and and  . .
However, according to the problem, these must be POSITIVE numbers, which rules out the second above.
The solution is 
and 
or 
or  = = 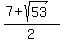
To check, show that their difference is 7 and their product is 1. (I sure don't want to post this so everyone can see, until I make sure that it works!!)
Difference = 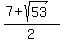 - - 
Difference = 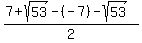 = =  = =
Product = 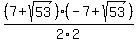 FOIL this out!! FOIL this out!!

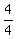 = = 
Final Answer: 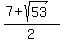 , , 
R^2 at SCC
|
|
|