Question 421228: find the vertex, the line of symmetry, the max or minimum value
of the quadratic function, and graph the function.
f(x) -2x^2 + 2x + 4
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the vertex, the line of symmetry, the max or minimum value
of the quadratic function, and graph the function.

the equation for a parabola can also be written in "vertex form":
 ....the vertex of the parabola is the point (h, k) ....the vertex of the parabola is the point (h, k)
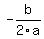 gives the gives the 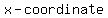 of the vertex of the vertex

so, 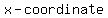 is is 
Substituting in the original equation to get the y-coordinate, we get:





So, the vertex of the parabola is at (1/2, 4.5).
| Solved by pluggable solver: Min/Max of a Quadratic Function |
The min/max of a quadratic equation is always at a point where its first differential is zero. This means that in our case, the value of  at which the given equation has a maxima/minima must satisfy the following equation: at which the given equation has a maxima/minima must satisfy the following equation:
=> 
This point is a minima if value of coefficient of x2 is positive and vice versa. For our function the point x=0.5 is a 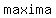 The graph of the equation is : The graph of the equation is :

Alternate method
In this method, we will use the perfect square method.
Step one:
Make the coefficient of  positive by multiplying it by positive by multiplying it by  in case in case . .
Maxima / Minima is decided from the sign of 'a'.
If 'a' is positive then we have Minima and for 'a'negative we have Maxima.
Step two:
Now make the perfect square with the same  and and  coefficient. coefficient.
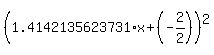
Maxima / Minima lies at the point where this squared term is equal to zero.
Hence,
=>
This point is a minima if value of coefficient of x2 is positive and vice versa. For our function the point x=0.5 is a  . .
For more on this topic, refer to Min/Max of a Quadratic equation. |
|
|
|