SOLUTION: Please, Please help me 2) For the function y = x2 - 4x - 5, perform the following tasks: a) Put the function in the form y = a(x - h)2 + k. Answer: Show work in this sp

Quadratic_Equations/41898 (2006-06-12 22:24:03): 
Please, Please help me 
2) For the function y = x2 - 4x - 5, perform the following tasks: 
a) Put the function in the form y = a(x - h)2 + k.
Answer: 
Show work in this space 

y = 1x² - 4x - 5

1. Factor coefficient of x² out of first two terms, using brackets:

                       y = 1[x² - 4x] - 5

2. To the side, calculate the number requires to complete the square:
     (I)  Multiply the coefficient of x by 1/2

         (-4)·(1/2) = -2 

    (II)  Square the result of (I)

         (-2)² = 4 

   (III)  Add this number and subtract it inside the brackets:

                      y = 1[x² - 4x + 4 - 4] - 5

3.  Inside the bracket, factor the trinomial consisting of the 
    first three terms, which should factor as a perfect square:

                      y = 1[(x - 2)(x - 2) - 4] - 5
            
                      y = 1[(x - 2)² - 4] - 5

4.  Remove the brackets, leaving the parentheses intact:

                      y = 1(x - 2)² - 4 - 5

5.  Combine the numbers

                      y = 1(x - 2)² - 9              

====================================================

Compare to            y = a(x - h)² + k

                    So a = 1, h = 2, k = -9

====================================================
                   
b) What is the line of symmetry?
Answer: 

The axis of symmetry of the graph (parabola) whose equation is

                      y = a(x - h)² + k

is the vertical line whose equation is x = h

Therefore the axis of symmetry of

                      y = 1(x - 2)² - 9              

is the vertical line whose equation is x = 2
                                  
c) Graph the function using the equation in part a. Explain why it is not necessary to plot points to graph when using y = a (x – h)2 + k.
Show graph here.

Explanation of graphing. 

The vertex of the equation is                 

                         y = a(x - h)² + k

is the point (h, k)

So the vertex of the equation is                 

                         y = 1(x - 2)² - 9

is the point (2, -9)

Plot that point:

 

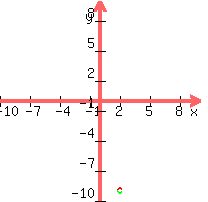Two additional points are (h-1, k+a) and (h+1, k+a)

There are (2-1, -9+1) and (2+1, -9+1) or (1,-8) and (3,-8)

Plot those two points:

 

Draw a U-shaped curve through them:

 


d) In your own words, describe how this graph compares to the graph of y = x2? 
Answer:

The graph of y = x² is 



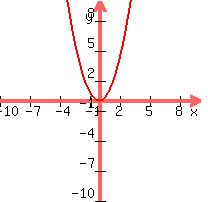It is shifted right h = 2 units (right) and k = -9 units (down)



Edwin
AnlytcPhil@aol.com