Question 399586: f(x) = −2x^2− 4x + 15 please do step by step so i can understand
1.Express the quadratic function in standard form. how did you get the numbers
F(x)=
2.vertex (x, y) = how did you get the numbers
3.x-intercepts (x, y) = Small value)
4.(x, y) = larger value)
5.y-intercept (x, y) =
graph and where do the numbers meet???
Thank you soo much...
Found 2 solutions by solver91311, edjones:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
\ =\ -2x^2\ -\ 4x\ +\ 15)
Standard form is:
\ =\ a\left(x\ -\ h\right)^2\ +\ k)
Where ) is the vertex. is the vertex.
Complete the square. Factor the lead coefficient from the terms with variables:
\ =\ -2\left(x^2\ +\ 2x\right)\ +\ 15)
Divide the coefficient on the first degree term by 2, square the result, and add that result INSIDE the parentheses. Compensate by adding the opposite of what you inserted inside the parentheses multiplied by the lead coefficient.
2 divided by 2 is 1, 1 squared is 1, add 1 inside the parentheses. -2 times 1 is -2, the opposite of -2 is 2, add 2 to the end.
\ =\ -2\left(x^2\ +\ 2x\ +\ 1\right)\ +\ 15\ +\ 2)
Factor the trinomial inside the parentheses and collect terms:
\ =\ -2\left(x\ +\ 1\right)^2\ +\ 17)
Paying careful attention to the signs, by inspection, the vertex is at )
The  -intercepts are the points where the graph of the function crosses the -intercepts are the points where the graph of the function crosses the  -axis. The -axis. The  -coordinates of the -coordinates of the  -intercepts are those values of -intercepts are those values of  that make the value of the function equal zero. Set the function equal to zero and solve. that make the value of the function equal zero. Set the function equal to zero and solve.
^2\ +\ 17\ =\ 0)
^2\ =\ -17)
^2\ =\ \frac{17}{2})



So the  -intercepts are -intercepts are ) and and )
The  -intercept is the value of the function when -intercept is the value of the function when  is zero. is zero.
\ =\ -2\left(0\ +\ 1\right)^2\ +\ 17\ =\ 15)
So the  -intercept is -intercept is )

Don't know what you mean by "where do the numbers meet" The Quadratic Club, or maybe at the Math Court at the Mall? I give up.
John

My calculator said it, I believe it, that settles it
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x)= −2x^2− 4x + 15
.
y intercept, when x=0 is 15
.
x intercepts when y=0:
x=(-2-sqrt(34))/2, x=(-2+sqrt(34))/2 See below.
.
f(x)=a(x-h)^2+k the standard form. The vertex is the point (h,k)=-2(x^2+2x)+15
=-2(x^2+2x+1-1)+15 completing the square
=-2(x^2+2x+1)+2+15
=-2(x+1)^2+17 the standard form.
a=-2, h=-1, k=17
.
(-1, 17) vertex.
.
Ed
.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=136 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 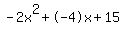 can be factored: can be factored:

Again, the answer is: -3.91547594742265, 1.91547594742265.
Here's your graph:
 |
|
|
|