Question 388219: another one...
The medians of the triangle are 6, 8, and 10. Find the sides.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First we construct a triangle ABC whose sides are the medians,
with AC = 6, BC = 8, and AB = 10
 Triangle ABC happens to be a right triangle, since 6² + 8² = 10², so
angle CBA has measure arccos(
Triangle ABC happens to be a right triangle, since 6² + 8² = 10², so
angle CBA has measure arccos( ) = arccos(.6) = arcsin(8/10)=arcsin(.8).
We will let AB be an actual median of the final triangle we are
going to create.
We know that the three medians intersect at a point which divides
each median into two parts such that the shorter part is ) = arccos(.6) = arcsin(8/10)=arcsin(.8).
We will let AB be an actual median of the final triangle we are
going to create.
We know that the three medians intersect at a point which divides
each median into two parts such that the shorter part is  of that median, and, of course, the longer part is
of that median, and, of course, the longer part is  of that
median.
So we locate point D such that AD is of that
median.
So we locate point D such that AD is  of AB and of course,
BD is of AB and of course,
BD is  of AB. So AD = of AB. So AD =  and BD = and BD =  Point D is where all three medians of our final triangle will intersect.
Point D is where all three medians of our final triangle will intersect.
 Next we must draw a median-to-be EF of the final triangle through D parallel
and equal to AC such that point D divides median-to be EF such that DF is
Next we must draw a median-to-be EF of the final triangle through D parallel
and equal to AC such that point D divides median-to be EF such that DF is
 of median-to be EF and DE is of median-to be EF and DE is  of median-to-be EF. Since
EF is 6, we will draw DF 2 units long and DE 4 units long: of median-to-be EF. Since
EF is 6, we will draw DF 2 units long and DE 4 units long:
 Next we will draw line segment EG through A so that AE = AG.
AG will be a side of the final triangle, and A will be the midpoint
of side EG of the final triangle.
Next we will draw line segment EG through A so that AE = AG.
AG will be a side of the final triangle, and A will be the midpoint
of side EG of the final triangle.
 Now we can calculate AE from triangle ADE by the law of cosines
since we have Side-Angle-Side We know that
side AD =
Now we can calculate AE from triangle ADE by the law of cosines
since we have Side-Angle-Side We know that
side AD =  ,
angle ADE = angle EAB because they are alternate interior angles formed
by transversal AB cutting parallel lines AC and EF.
So angle ADE = arccos(.6)
side DE = 4 ,
angle ADE = angle EAB because they are alternate interior angles formed
by transversal AB cutting parallel lines AC and EF.
So angle ADE = arccos(.6)
side DE = 4






 And since A is the midpoint of EG,
side EG of the final triangle is twice that or
side EG =
And since A is the midpoint of EG,
side EG of the final triangle is twice that or
side EG =  . That's one of the sides of the final triangle.
Now if we have drawn everything right so far, points G, F, and B
should be colinear and GB should be a side of the final triangle,
with F at its midpoint. . That's one of the sides of the final triangle.
Now if we have drawn everything right so far, points G, F, and B
should be colinear and GB should be a side of the final triangle,
with F at its midpoint.
 Next we must calculate FG. But to do that we must calculate
angle E.
We will use the law of sines in triangle ADE.
Next we must calculate FG. But to do that we must calculate
angle E.
We will use the law of sines in triangle ADE.

 So angle E = arcsin(.8) = arccos(.6)
Now we can calculate FG by the law of cosines, since we have
side-angle-side.
EG =
So angle E = arcsin(.8) = arccos(.6)
Now we can calculate FG by the law of cosines, since we have
side-angle-side.
EG =  , angle E = arccos(.6), EF = 6 , angle E = arccos(.6), EF = 6





 And since F is the midpoint of BG,
side BG of the final triangle is twice that or
side BG =
And since F is the midpoint of BG,
side BG of the final triangle is twice that or
side BG = 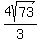 . That's another side of the final triangle.
There is just one more side to find, and that is BE, which we will now
draw in: . That's another side of the final triangle.
There is just one more side to find, and that is BE, which we will now
draw in:
 We have now completed the final triangle BEG. We only need side BE.
We can find it by the law of cosines since we have side-angle-side
in triangle BDE.
Side DE = 4,
Angle BDE is supplementary to angle ADE and so its cosine is the
negative of the cosine of angle ADE, so angle BDE = arccos(-.6)
Side BD =
We have now completed the final triangle BEG. We only need side BE.
We can find it by the law of cosines since we have side-angle-side
in triangle BDE.
Side DE = 4,
Angle BDE is supplementary to angle ADE and so its cosine is the
negative of the cosine of angle ADE, so angle BDE = arccos(-.6)
Side BD = 




 So we have found all three sides of triangle BEG.
We didn't draw in the third median, but we don't need to.
Edwin
So we have found all three sides of triangle BEG.
We didn't draw in the third median, but we don't need to.
Edwin
|
|
|