SOLUTION: how do you complete the square, y=8-3x^2-2x (3x^2)is suppose to be 3x squared

Arrange the right side in descending order:



Factor -3 out of the first two terms on the right:



[Note that I got the 
 by dividing -2 by -3]


To the side multiply the coefficient of x, which is  by ,
which gives  then square it, getting , then add and
subtract  after the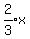 



Notice that the first three terms inside the parentheses, 
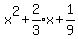 can be factored as  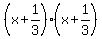and
then as 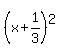.  So replace the first three terms by this:




Remove the larger outside parentheses leaving the smaller parentheses
intact:



Reduce  to 



To add the last two terms:  , so
the final answer is:



Compare that to



and , , 

so the vertex is the point 

the line of symmetry has the equation  or .

We know it opens downward since "a" is a negative number.

We find the y-intercept by substituting x = 0 in the original

equation:






So the y-intecept is (0,8), 

We find the x-intercepts from the original equation,
setting y=0





Rewrite as



Multiply through by -1





 gives 

 gives 

So the x-intercepts are the points (,0) and (-2,0)


so we plot the vertex, the y-intercept, the x-intercepts,
and the vertical line of symmetry:



and sketch in the parabola graph, through those points,
symmetrical about the green line of symmetry:



Edwin